
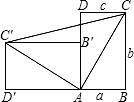
 一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的验证方法.如图,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′,设AB=a,BC=b,AC=c,请利用四边形BCC′D′的面积验证勾股定理:a2+b2=c2.
一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的验证方法.如图,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′,设AB=a,BC=b,AC=c,请利用四边形BCC′D′的面积验证勾股定理:a2+b2=c2.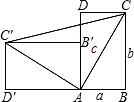 证明:四边形BCC′D′为直角梯形,
证明:四边形BCC′D′为直角梯形, (BC+C′D′)•BD′=
(BC+C′D′)•BD′=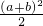 ,
, ab+
ab+ c2+
c2+ ab=
ab=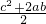 ;
;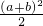 =
=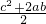 ;
;

 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
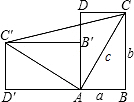 一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的验证方法.如图,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′,设AB=a,BC=b,AC=c,请利用四边形BCC′D′的面积验证勾股定理:a2+b2=c2.
一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的验证方法.如图,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′,设AB=a,BC=b,AC=c,请利用四边形BCC′D′的面积验证勾股定理:a2+b2=c2.查看答案和解析>>
科目:初中数学 来源: 题型:
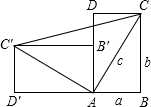 侧面ABCD(是一个长方形)倒下到AB′C′D′的位置,连接CC′,设AB=a,BC=b,AC=c.
侧面ABCD(是一个长方形)倒下到AB′C′D′的位置,连接CC′,设AB=a,BC=b,AC=c.查看答案和解析>>
科目:初中数学 来源:2012年人教版八年级下第十八章勾股定理第一节勾股定理1练习卷(解析版) 题型:解答题
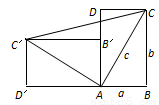
一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的验证方法.如图,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′,设AB=a,BC=b,AC=c,请利用四边形BCC′D′的面积验证勾股定理:a2+b2=c2.
查看答案和解析>>
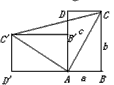
科目:初中数学 来源:期末题 题型:解答题
查看答案和解析>>
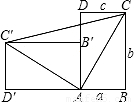
科目:初中数学 来源:2004年湖北省荆门市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com