
分析 根据分式的减法和除法可以化简题目中的式子,然后将x的值代入即可解答本题.
解答 解:($\frac{3x-1}{x-1}$-x-1)÷$\frac{{x}^{2}-6x+9}{x-1}$
=$\frac{3x-1-(x+1)(x-1)}{x-1}•\frac{x-1}{(x-3)^{2}}$
=$\frac{3x-1-{x}^{2}+1}{x-1}•\frac{x-1}{(x-3)^{2}}$
=$\frac{-x(x-3)}{x-1}•\frac{x-1}{(x-3)^{2}}$
=$\frac{x}{3-x}$,
当x=$\sqrt{3}$+3时,原式=$\frac{\sqrt{3}+3}{3-\sqrt{3}-3}=-\frac{\sqrt{3}+3}{\sqrt{3}}=-1-\sqrt{3}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.


科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,AD=1,则BD的长为( )
如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,AD=1,则BD的长为( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
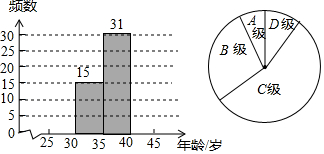 菲尔兹奖是国际上享有崇高声誉的一个数学奖项,每4年评选一次,颁给有卓越贡献的年轻数学家,被视为数学界的诺贝尔奖.下面的数据是从1936年至2014年45岁以下菲尔兹奖得住获奖时的年龄(岁):
菲尔兹奖是国际上享有崇高声誉的一个数学奖项,每4年评选一次,颁给有卓越贡献的年轻数学家,被视为数学界的诺贝尔奖.下面的数据是从1936年至2014年45岁以下菲尔兹奖得住获奖时的年龄(岁):| 分组 | 频数 |
| A:25~30 | 1 |
| B:30~35 | 15 |
| C:35~40 | 31 |
| D:40~45 | 3 |
| 总 计 | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
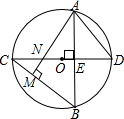 如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.
如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{x}^{2}{y}^{2}}$ | B. | $\sqrt{{x}^{2}+{y}^{2}}$ | C. | $\sqrt{(x+y)^{2}}$ | D. | $\sqrt{x{y}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
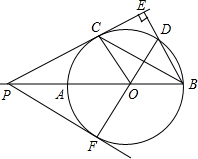 如图,AB是⊙O的直径,延长BA至点P,过点P作⊙O的切线PC,切点为C,过点B向PC的延长线作垂线BE交该延长线于点E,BE交⊙O于点D,已知PA=1,PC=$\sqrt{3}$OC,
如图,AB是⊙O的直径,延长BA至点P,过点P作⊙O的切线PC,切点为C,过点B向PC的延长线作垂线BE交该延长线于点E,BE交⊙O于点D,已知PA=1,PC=$\sqrt{3}$OC,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com