
°æƒø°øœ÷”–“ª∏ˆ÷÷÷≤◊‹√ʪ˝Œ™540m2µƒæÿ–ŒÀ‹¡œŒ¬≈Ô£¨∑÷¬¢º‰∏ÙÃ◊÷÷≤››Æ∫ÕŒ˜∫Ï ¡π≤24¬¢£¨÷÷÷≤µƒ≤››ÆªÚŒ˜∫Ï ¡µ•÷÷≈©◊˜ŒÔµƒ◊‹¬¢ ˝≤ªµÕ”⁄10¬¢£¨”÷≤ª≥¨π˝14¬¢(¬¢ ˝Œ™’˝’˚ ˝)£¨À¸√«µƒ’ºµÿ√ʪ˝°¢≤˙¡ø°¢¿˚»Û∑÷±»Áœ¬£∫
’ºµÿ√ʪ˝£®m/¬¢£© | ≤˙¡ø£®«ßøÀ/¬¢£© | ¿˚»Û£®‘™/«ßøÀ£© | |
Œ˜∫Ï ¡ | 30 | 160 | 1.1 |
≤››Æ | 15 | 50 | 1.6 |
£®1£©»Ù…Ë≤››Æπ≤÷÷÷≤¡À![]() ¬¢£¨Õ®π˝º∆À„Àµ√˜π≤”–º∏÷÷÷÷÷≤∑Ω∞∏£ø∑÷± «ƒƒº∏÷÷£ø
¬¢£¨Õ®π˝º∆À„Àµ√˜π≤”–º∏÷÷÷÷÷≤∑Ω∞∏£ø∑÷± «ƒƒº∏÷÷£ø
£®2£©‘⁄’‚º∏÷÷÷÷÷≤∑Ω∞∏÷–£¨ƒƒ÷÷∑Ω∞∏ªÒµ√µƒ¿˚»Û◊Ó¥Û£ø◊Ó¥Û¿˚»Û «∂‡…Ÿ£ø
°æ¥∞∏°øΩ‚£∫£®1£©∏˘æ›Ã‚“‚Œ˜∫Ï ¡÷÷¡À£®24-![]() £©¬¢
£©¬¢
15![]() +30(24-
+30(24-![]() )°‹540 Ω‚µ√
)°‹540 Ω‚µ√![]() °›12
°›12
°fl![]() °‹14£¨«“
°‹14£¨«“![]() «’˝’˚ ˝ °‡
«’˝’˚ ˝ °‡![]() =12£¨13£¨14
=12£¨13£¨14
π≤”–»˝÷÷÷÷÷≤∑Ω∞∏£¨∑÷± «£∫
∑Ω∞∏“ª£∫≤››Æ÷÷÷≤12¬¢£¨Œ˜∫Ï ¡÷÷÷≤12¬¢
∑Ω∞∏∂˛£∫≤››Æ÷÷÷≤13¬¢£¨Œ˜∫Ï ¡÷÷÷≤11¬¢
∑Ω∞∏»˝£∫≤››Æ÷÷÷≤14¬¢£¨Œ˜∫Ï ¡÷÷÷≤10¬¢
£®2£©Ω‚∑®“ª£∫∑Ω∞∏“ªªÒµ√µƒ¿˚»Û£∫12°¡50°¡1.6+12°¡160°¡1.1=3072£®‘™£©
∑Ω∞∏∂˛ªÒµ√µƒ¿˚»Û£∫13°¡50°¡1.6+11°¡160°¡1.1=2976£®‘™£©
∑Ω∞∏»˝ªÒµ√µƒ¿˚»Û£∫14°¡50°¡1.6+10°¡160°¡1.1=2880£®‘™£©
”…º∆À„÷™£¨÷÷÷≤Œ˜∫Ï ¡∫Õ≤››Æ∏˜12¬¢£¨ªÒµ√µƒ¿˚»Û◊Ó¥Û£¨
◊Ó¥Û¿˚»Û «3072‘™
Ω‚∑®∂˛£∫»Ù≤››Æ÷÷¡À![]() ¬¢£¨…Ë÷÷÷≤≤››Æ∫ÕŒ˜∫Ï ¡π≤ø…ªÒµ√¿˚»Û
¬¢£¨…Ë÷÷÷≤≤››Æ∫ÕŒ˜∫Ï ¡π≤ø…ªÒµ√¿˚»Û![]() ‘™£¨‘Ú
‘™£¨‘Ú
![]()
°fl![]() -96£º0 °‡
-96£º0 °‡![]() ÀÊ
ÀÊ![]() µƒ‘ˆ¥Û∂¯ºı–°
µƒ‘ˆ¥Û∂¯ºı–°
”÷°fl12°‹![]() °‹14£¨«“
°‹14£¨«“![]() «’˝’˚ ˝
«’˝’˚ ˝
°‡µ±![]() =12 ±£¨
=12 ±£¨![]() =3072£®‘™£©
=3072£®‘™£©
°æΩ‚Œˆ°ø
£®1£©¡–≥ˆ“ª‘™“ª¥Œ≤ªµ» Ω◊È£¨«Û≥ˆ≤››Æ÷÷÷≤¬¢ ˝µƒ»°÷µ∑∂Œß£¨æÕø…“‘’“≥ˆ∑Ω∞∏£ª
£®2£©¡–≥ˆ“ª¥Œ∫Ø ˝£¨¥˙»Î∑Ω∞∏÷–µƒ ˝æ›£¨Ω¯––±»Ωœ£¨ø…“‘’“≥ˆ¥∞∏£Æ



| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∞¥÷∏∂®µƒ∑Ω∑®Ω‚œ¬¡–∑Ω≥Ã:
£®1£©![]() (≈‰∑Ω∑®)£ª
(≈‰∑Ω∑®)£ª
£®2£©![]() (“Ú Ω∑÷Ω‚∑®) £Æ
(“Ú Ω∑÷Ω‚∑®) £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº ¢≈![]() µƒ∆Ω∑÷œfl∫ÕÕ‚Ω«
µƒ∆Ω∑÷œfl∫ÕÕ‚Ω«![]() µƒ∆Ω∑÷œflœ‡Ωª”⁄
µƒ∆Ω∑÷œflœ‡Ωª”⁄![]() µ„£¨
µ„£¨![]() °£
°£
£®1£©«Û![]() µƒ∂» ˝£ª£®–¥¿Ì”…£©
µƒ∂» ˝£ª£®–¥¿Ì”…£©
£®2£©»ÁÕº£®2£©£¨‘⁄¢≈µƒÃıº˛œ¬£¨‘Ÿª≠![]() ∫Õ
∫Õ![]() µƒΩ«∆Ω∑÷œflœ‡Ωª”⁄
µƒΩ«∆Ω∑÷œflœ‡Ωª”⁄![]() µ„£¨«Û
µ„£¨«Û![]() µƒ∂» ˝£ª
µƒ∂» ˝£ª
£®3£©»Ù![]() £¨∞¥…œ ˆπʬ…ºÃ–¯ª≠œ¬»•£¨«Î÷±Ω”–¥≥ˆ
£¨∞¥…œ ˆπʬ…ºÃ–¯ª≠œ¬»•£¨«Î÷±Ω”–¥≥ˆ![]() µƒ∂» ˝°£
µƒ∂» ˝°£

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øªØºÚ≤¢«Û÷µ
£®1£©5x2y+[7xy©Å2£®3xy©Å2x2y£©©Åxy]£¨∆‰÷–x£Ω©Å1£¨y£Ω©Å![]()
£®2£©“—÷™a2©Åa©Å2£Ω0£¨«Ûa2©Å2£®a2©Åa+3£©©Å![]() £®a2©Åa©Å4£©µƒ÷µ£Æ
£®a2©Åa©Å4£©µƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
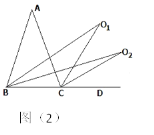
°æƒø°ø»ÁÕº£¨“—÷™![]() ABCD ÷–£¨°œBDC£Ω45°„£¨BE°ÕCD ”⁄ E£¨DG°ÕBC ”⁄ G£¨BE°¢DG œ‡Ωª”⁄ H£¨DG°¢AB µƒ—”≥§œfl œ‡Ωª”⁄ F£¨œ¬√ÊΩ·¬€£∫¢Ÿ°œA£Ω°œDHE£ª¢⁄°˜DCG°’°˜BCE£ª¢€AD£ΩDH£ª¢‹DH=HF∆‰÷–’˝»∑µƒΩ·¬€”–________£®÷ªÃÓ’˝»∑Ω·¬€µƒ–Ú∫≈£©£Æ
ABCD ÷–£¨°œBDC£Ω45°„£¨BE°ÕCD ”⁄ E£¨DG°ÕBC ”⁄ G£¨BE°¢DG œ‡Ωª”⁄ H£¨DG°¢AB µƒ—”≥§œfl œ‡Ωª”⁄ F£¨œ¬√ÊΩ·¬€£∫¢Ÿ°œA£Ω°œDHE£ª¢⁄°˜DCG°’°˜BCE£ª¢€AD£ΩDH£ª¢‹DH=HF∆‰÷–’˝»∑µƒΩ·¬€”–________£®÷ªÃÓ’˝»∑Ω·¬€µƒ–Ú∫≈£©£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
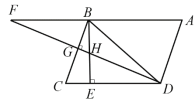
°æƒø°ø»ÁÕºÀ˘ 棨 ˝÷·…œµƒµ„A£¨B£¨C£¨D±Ì 浃 ˝∑÷±Œ™£∫£≠1.5£¨£≠3,2,3.5.
![]()
(1)Ω´A£¨B£¨C£¨D±Ì 浃 ˝∞¥¥”–°µΩ¥ÛµƒÀ≥–Ú”√°∞£º°±∫≈¡¨Ω”∆¿¥£ª
(2)»ÙΩ´‘≠µ„∏ƒ‘⁄Cµ„£¨∆‰”‡∏˜µ„À˘∂‘”¶µƒ ˝∑÷±Œ™∂‡…Ÿ£øΩ´’‚–© ˝∞¥¥”–°µΩ¥ÛµƒÀ≥–Ú”√°∞£º°±¡¨Ω”∆¿¥£ª
(3)∏ƒ±‰‘≠µ„Œª÷√∫Û£¨µ„A£¨B£¨C£¨DÀ˘±Ì 浃 ˝¥Û–°À≥–Ú∏ƒ±‰¡À¬£ø’‚Àµ√˜¡À ˝÷·µƒ ≤√¥–‘÷ £ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™÷±œfl y13x 6”Î x ÷·°¢y ÷·∑÷±Ωª”⁄µ„ A£¨C£ªπ˝µ„ C µƒ÷±œfl y2x b ”Î x ÷·Ωª”⁄µ„ B£Æ
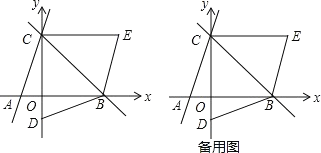
£®1£©b µƒ÷µŒ™ £ª
£®2£©»Ùµ„ D µƒ◊¯±ÍŒ™£®0£¨©Å2£©£¨Ω´°˜BCD —ÿ÷±œfl BC ∂‘’€∫Û£¨µ„ D ¬‰µΩµ⁄“ªœÛœfiµƒµ„ E ¥¶£¨ «Û÷§£∫Àƒ±fl–Œ ABEC «∆Ω––Àƒ±fl–Œ£ª
£®3£©‘⁄÷±œfl BC …œ «∑ҥʑ⁄µ„ P£¨ πµ√“‘ P°¢A°¢D°¢B Œ™∂•µ„µƒÀƒ±fl–Œ «∆Ω––Àƒ±fl–Œ£ø »Áπ˚¥Ê‘⁄£¨«Î«Û≥ˆµ„ P µƒ◊¯±Í£ª»Áπ˚≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨Ω´°˜ABC—ÿ…‰œflBC∑ΩœÚ∆Ω“∆3cmµ√µΩ°˜DEF£Æ»Ù°˜ABCµƒ÷‹≥§Œ™14cm£¨‘ÚÀƒ±fl–ŒABFDµƒ÷‹≥§Œ™£®°°°°£©
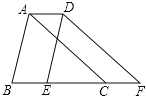
A. 14cm B. 17cm C. 20cm D. 23cm
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄°∞º“µÁœ¬œÁ°±ªÓ∂Ø∆⁄º‰£¨∑≤π∫¬Ú÷∏∂®º“”√µÁ∆˜µƒ≈©¥Âæ”√Òæ˘ø…µ√µΩ∏√…Ã∆∑ €º€13%µƒ≤∆’˛≤πÃ˘£Æ¥Â√Ò–°¿Óπ∫¬Ú¡À“ªÃ®A–Õœ¥“¬ª˙£¨–°Õıπ∫¬Ú¡À“ªÃ®B–Õœ¥“¬ª˙¡Ω»À“ªπ≤µ√µΩ≤∆’˛≤πÃ˘351‘™£¨”÷÷™B–Õœ¥“¬ª˙ €º€±»A–Õœ¥“¬ª˙ €º€∂‡500‘™£Æ«Û£∫
£®1£©A–Õœ¥“¬ª˙∫ÕB–Õœ¥“¬ª˙µƒ €º€∏˜ «∂‡…Ÿ‘™?
£®2£©–°¿Ó∫Õ–°Õıπ∫¬Úœ¥“¬ª˙≥˝≤∆’˛≤πÃ˘Õ‚ µº ∏˜∏∂øÓ∂‡…Ÿ‘™£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com