
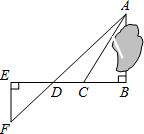
 为了测量被池塘隔开的A、B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据:①BC,∠ACB; ②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.根据所测数据,能出A,B间距离的有①②③(填上所有能求出A、B间距离的序号)
为了测量被池塘隔开的A、B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据:①BC,∠ACB; ②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.根据所测数据,能出A,B间距离的有①②③(填上所有能求出A、B间距离的序号) 分析 利用正切的定义可由①求出AB;利用正切的定义表示求出BD、BC,再利用CD=$\frac{x}{tan∠ADB}$-$\frac{x}{tan∠ACB}$,则求出AB,于是可对②进行判断;利用相似三角形的判定与性质可对③④进行判断.
解答 解:当已知BC,∠ACB:
在Rt△ABC,∵tan∠ACB=$\frac{AB}{BC}$,
∴AB=BCtan∠ACB;
当已知CD,∠ACB,∠ADB,设AB=x,
∵tan∠ADB=$\frac{AB}{BD}$,
∴BD=$\frac{x}{tan∠ADB}$,
∵tan∠ACB=$\frac{AB}{BC}$,
∴BC=$\frac{x}{tan∠ACB}$,
∴DB-BC=CD,即CD=$\frac{x}{tan∠ADB}$-$\frac{x}{tan∠ACB}$,
∴x=$\frac{CD•tan∠ACB•tan∠ADB}{tan∠ACB-tan∠ADB}$;
当已知EF,DE,BD,则证明△ABD∽△FED,所以$\frac{AB}{EF}$=$\frac{BD}{DE}$,即AB=$\frac{BD•EF}{DE}$;
当已知DE,DC,BC不能求出AB.
故答案①②③.
点评 本题考查了相似三角形的应用:常常构造“A”型或“X”型相似图,三点应在一条直线上.必须保证在一条直线上,为了使问题简便,尽量构造直角三角形.也考查了解直角三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
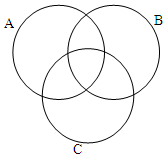 已知A、B、C三个数集,每个数集中所包含的数都写在各自的大括号内,请把这些数填在如图所示圈内的相应位置.
已知A、B、C三个数集,每个数集中所包含的数都写在各自的大括号内,请把这些数填在如图所示圈内的相应位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 速度v | 40 | 60 |
| 路程s | 40 | 70 |
| 指数P | 1000 | 1600 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$ | B. | $\sqrt{0.2}$ | C. | $\sqrt{\frac{2}{5}}$ | D. | $\sqrt{\frac{8}{25}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com