
分析 先将分母中两个二次根式化简,再进行分母有理化,从而发现每个分母均为4,最后计算分子的和,即可得答案.
解答 解:原式=$\frac{1}{\sqrt{1+{2}^{2}}+\sqrt{1}}$+$\frac{1}{\sqrt{1+\frac{9}{4}}+\sqrt{1+\frac{1}{4}}}$+$\frac{1}{\sqrt{1+\frac{16}{9}}+\sqrt{1+\frac{4}{9}}}$+…+$\frac{1}{\sqrt{1+\frac{441}{400}}+\sqrt{1+\frac{361}{400}}}$
=$\frac{1}{\sqrt{5}+1}$+$\frac{1}{\frac{\sqrt{13}}{2}+\frac{\sqrt{5}}{2}}$+$\frac{1}{\frac{5}{3}+\frac{\sqrt{13}}{3}}$+…+$\frac{1}{\frac{29}{20}+\frac{\sqrt{761}}{20}}$
=$\frac{1}{\sqrt{5}+1}$+$\frac{2}{\sqrt{13}+\sqrt{5}}$+$\frac{3}{5+\sqrt{13}}$+…+$\frac{20}{29+\sqrt{761}}$
=$\frac{\sqrt{5}-1}{4}$+$\frac{2(\sqrt{13}-\sqrt{5})}{8}$+$\frac{3(\sqrt{25}-\sqrt{13})}{12}$+…+$\frac{20(29-\sqrt{761})}{80}$
=$\frac{\sqrt{5}-1}{4}$+$\frac{\sqrt{13}-\sqrt{5}}{4}$+$\frac{\sqrt{25}-\sqrt{13}}{4}$+…+$\frac{29-\sqrt{761}}{4}$
=$\frac{\sqrt{5}-1+\sqrt{13}-\sqrt{5}+\sqrt{25}-\sqrt{13}+…+29-\sqrt{761}}{4}$
=$\frac{-1+29}{4}$
=7,
故答案为:7.
点评 本题主要考查二次根式的加减法,熟练掌握二次根式的运算顺序和运算法则是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
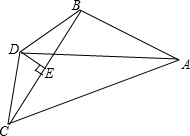 如图,在△ABC中,AC>AB,AD平分∠BAC,点D到点B与点C的距离相等,过点D作DE⊥BC于点E.
如图,在△ABC中,AC>AB,AD平分∠BAC,点D到点B与点C的距离相等,过点D作DE⊥BC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com