
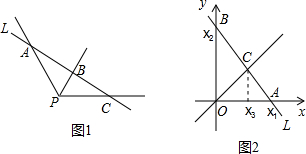
���� ��1����ͼ1�У�����B��BE��PA��PC�ڵ�E����BE��PA���Ƴ���BEC�ס�APC���õ�$\frac{BE}{AP}$=$\frac{EC}{PC}$����$\frac{{x}_{3}}{{x}_{1}}$=$\frac{{x}_{2}-{x}_{3}}{{x}_{2}}$����x2x3+x1x3=x1x2�����߳���x1x2x3���ɽ�����⣮
��2����ͼ2�У�����C��CD��x���ڵ�D��CE��y���ڵ�E����S��BOC+S��AOC=S��AOB���г�ʽ�ӣ����ɽ�����⣮
��� ��1��֤������ͼ1�У�����B��BE��PA��PC�ڵ�E��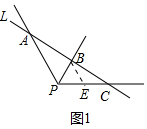
��BE��PA��
���BEC�ס�APC��
�ߡ�APC=120�㣬PBƽ�֡�APC���ɵá�PBE�ǵȱ������Σ�
��BE=PE=PB=x3��
��EC=x2-x3��
��$\frac{BE}{AP}$=$\frac{EC}{PC}$��
��$\frac{{x}_{3}}{{x}_{1}}$=$\frac{{x}_{2}-{x}_{3}}{{x}_{2}}$��
��x2x3+x1x3=x1x2��
��$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{1}{{x}_{3}}$��
�ڽ⣺��ͼ2�У�����C��CD��x���ڵ�D��CE��y���ڵ�E��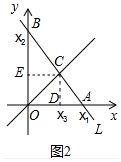
�ߵ�C��ֱ��y=x�ϣ��Һ�����Ϊx3�����C��x3��x3����
��CE=CD=x3��
��S��BOC+S��AOC=S��AOB��
��$\frac{1}{2}$x2x3+$\frac{1}{2}$x1x3=$\frac{1}{2}$x1x2��
��$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{1}{{x}_{3}}$��
���� ���⿼��һ�κ����ۺ��⡢���������ε��ж������ʡ������ε������֪ʶ������Ĺؼ������Ӧ����ѧ֪ʶ������⣬ѧ�����ӳ��ø����ߣ��������������ν�����⣬�����п�ѹ���⣮


 ��ǿ��У��ĩ���100��ϵ�д�
��ǿ��У��ĩ���100��ϵ�д� �óɼ�1��1��ĩ���100��ϵ�д�
�óɼ�1��1��ĩ���100��ϵ�д� ��״Ԫ���źþ�ϵ�д�
��״Ԫ���źþ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
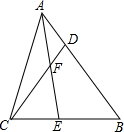 ��֪����ͼ���ڡ�ABC�У�AE�ǽ�ƽ���ߣ�D��AB�ϵĵ㣬AE��CD�ཻ�ڵ�F��
��֪����ͼ���ڡ�ABC�У�AE�ǽ�ƽ���ߣ�D��AB�ϵĵ㣬AE��CD�ཻ�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ����ˮ���ۼ۸� | ��ˮ�����۸� | |
| ÿ��ÿ����ˮ�� | ���ۣ�Ԫ/�� | ���ۣ�Ԫ/�� |
| 17�ּ����� | a | 0.80 |
| ����17�ֵ�������30�ֵIJ��� | b | 0.80 |
| ����30�ֵIJ��� | 6.00 | 0.80 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
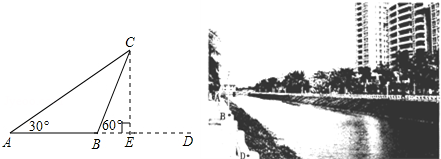
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
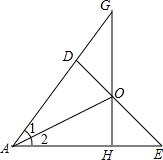 ��֪����ͼ��OD��AD��OH��AE��DE��GH��O��
��֪����ͼ��OD��AD��OH��AE��DE��GH��O���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
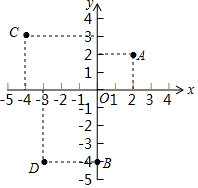 д����ͼ��ʾ��ƽ��ֱ������ϵ��A��B��C��D������꣬���ֱ�ָ���������ڵ����ޣ�
д����ͼ��ʾ��ƽ��ֱ������ϵ��A��B��C��D������꣬���ֱ�ָ���������ڵ����ޣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com