
【题目】如图,在等边三角形△ABC中,AE=CD,AD、BE交于P点,BQ⊥AD于Q,求证:
(1) BP=2PQ
(2) 连PC,若BP⊥PC,求![]() 的值
的值

【答案】(1)证明见解析;(2)1.
【解析】
(1)根据全等三角形的判定定理SAS可得△BAE≌△ACD,得∠ABE=∠CAD,即可得出∠BPQ=60°,再根据BQ⊥AD,得出BP=2PQ;
(2)根据∠ABE=∠CAD,得∠PBC=∠BAQ,利用AAS可证明△BAQ≌△CBP,从而得出AP=PQ,即可得出![]() 的值.
的值.
(1)证明:在等边△ABC中
AB=AC,∠BAE=∠ACD=60°
在△BAE和△ACD中,
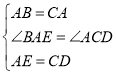
∴△BAE≌△ACD(SAS),
∴∠ABE=∠CAD,
∴∠BPQ=∠ABE+∠BAP=∠CAD+∠BAP=∠BAC=60°,
∵BQ⊥AD于Q
∴∠PBQ=30°
∴BP=2PQ
(2) ∵∠ABE=∠CAD,
∴∠ABC∠ABE=∠BAC∠CAD,
即∠PBC=∠BAQ,
在△BAQ和△CBP中,

∴△BAQ≌△CBP(AAS),
∴AQ=BP=2PQ,
∴AP=PQ,
即![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中AB=AC.
(1)作图:在AC上有一点D,延长BD,并在BD的延长线上取点E,使AE=AB,连AE,作∠EAC的平分线AF,AF交DE于点F(用尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,连接CF,求证:∠BAC=∠BFC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在全省各大景区都在流行“真人CS“娱乐项目,其中有一个“快速抢点”游戏,游戏规则:如图,用绳子围成的一个边长为10m的正方形ABCD场地中,游戏者从AB边上的点E处出发,分别先后赶往边BC、CD、DA上插小旗子,最后回到点![]() 已知
已知![]() ,则游戏者所跑的最少路程是多少______
,则游戏者所跑的最少路程是多少______![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从相距420km的A、B两地相向而行,乙车比甲车先出发1小时,两车分别以各自的速度匀速行驶,途经C地(A、B、C三地在同一条直线上).甲车到达C地后因有事立即按原路原速返回A地,乙车从B地直达A地,甲、乙两车距各自出发地的路程y(千米)与甲车行驶所用的时间x(小时)的关系如图所示,结合图象信息回答下列问题:
(1)甲车的速度是 千米/时,乙车的速度是 千米/时;
(2)求甲车距它出发地的路程y(千米)与它行驶所用的时间x(小时)之间的函数关系式;
(3)甲车出发多长时间后两车相距90千米?请你直接写出答案.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,M、N分别是边OA、OB上的定点,P、Q分别是边OB、OA上的动点,记∠AMP=∠1,∠ONQ=∠2,当MP+PQ+QN最小时,则关于∠1、∠2的数量关系正确的是( )

A.∠1+∠2=90°B.2∠2-∠1=30°
C.2∠1+∠2=180°D.∠1-∠2=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应南充市创建“全国卫生城市”的号召,某校1 500名学生参加了卫生知识竞赛,成绩记为A、B、C、D四等。从中随机抽取了部分学生成绩进行统计,绘制成如下两幅不完整的统计图表,根据图表信息,以下说法不正确的是( )
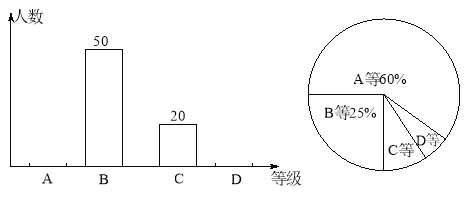
A.样本容量是200
B.D等所在扇形的圆心角为15°
C.样本中C等所占百分比是10%
D.估计全校学生成绩为A等大约有900人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】热爱学习的小明同学在网上搜索到下面的文字材料:
在x轴上有两个点它们的坐标分别为![]() 和
和![]() .则这两个点所成的线段的长为
.则这两个点所成的线段的长为![]() ;同样,若在y轴上的两点坐标分别为(0,b)和(0,d),则这两个点所成的线段的长为|b-d|.如图1,在直角坐标系中的任意两点P1,P2,其坐标分别为(a,b)和(c,d),分别过这两个点作两坐标轴的平行线,构成一个直角三角形,其中直角边P1Q=|a-c|,P2Q=|b-d|,利用勾股定理可得,线段P1 P2的长为
;同样,若在y轴上的两点坐标分别为(0,b)和(0,d),则这两个点所成的线段的长为|b-d|.如图1,在直角坐标系中的任意两点P1,P2,其坐标分别为(a,b)和(c,d),分别过这两个点作两坐标轴的平行线,构成一个直角三角形,其中直角边P1Q=|a-c|,P2Q=|b-d|,利用勾股定理可得,线段P1 P2的长为![]() .
.

根据上面材料,回答下面的问题:
(1)在平面直角坐标系中,已知![]() ,
,![]() ,则线段AB的长为_____;
,则线段AB的长为_____;
(2)若点C在y轴上,点D的坐标是![]() ,且
,且![]() ,则点C的坐标是_____;
,则点C的坐标是_____;
(3)如图2,在直角坐标系中,点A,B的坐标分别为![]() 和
和![]() ,点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,求△ABC周长的最小值.
,点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,求△ABC周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,P是抛物线y=-x2+3x上一点,且在x轴上方,过点P分别向x轴、y轴作垂线,得到矩形PMON.若矩形PMON的周长随点P的横坐标m增大而增大,则m的取值范围是_________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com