
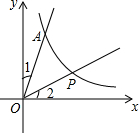
 如图,直线y=3x和双曲线y=$\frac{3}{x}$(x>0)交于点A,点P为双曲线上一点,且∠POA=∠1+∠2,求点P的坐标.
如图,直线y=3x和双曲线y=$\frac{3}{x}$(x>0)交于点A,点P为双曲线上一点,且∠POA=∠1+∠2,求点P的坐标. 分析 过点A作x平行线交y轴于点E,过点P作y轴的平行线交x轴于点F,交EA于点B,连接AP.将一次函数解析式代入到反比例函数解析式中解方程得出点A的坐标,再根据∠POA=∠1+∠2,且∠POA+∠1+∠2=90°,设出点P的坐标,利用分解图形法求出△AOP的面积,再结合三角形的面积公式以及∠AOP=45°,即可求出点P的横坐标,将其代入到点P的坐标中即可得出结论.
解答 解:过点A作x平行线交y轴于点E,过点P作y轴的平行线交x轴于点F,交EA于点B,连接AP.如图所示.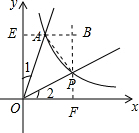
将一次函数解析式y=3x代入到反比例函数解析式y=$\frac{3}{x}$(x>0)中,
3x=$\frac{3}{x}$,即3x2=3,
解得:x=1,或x=-1(舍去).
当x=1时,y=$\frac{3}{1}$=3,
∴点A的坐标为(1,3).
设点P的坐标为(n,$\frac{3}{n}$)(n>0),
则OF=n,OE=3,BP=3-$\frac{3}{n}$,AB=n-1,OA=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,OP=$\sqrt{{n}^{2}+(\frac{3}{n})^{2}}$.
∵∠POA=∠1+∠2,且∠POA+∠1+∠2=90°,
∴∠POA=45°.
SPOA=S矩形OFBE-S△OAE-S△OPF-S△ABP=3n-$\frac{3}{2}$-$\frac{3}{2}$-$\frac{1}{2}$(3-$\frac{3}{n}$)(n-1)=$\frac{3}{2}$(1+$\frac{1}{n}$)(n-1)=$\frac{3}{2}$(n-$\frac{1}{n}$).
又∵SPOA=$\frac{1}{2}$OA•OP•sin∠POA=$\frac{\sqrt{5}}{2}$$\sqrt{{n}^{2}+(\frac{3}{n})^{2}}$=$\frac{3}{2}$(n-$\frac{1}{n}$),
即4n4-18n2-36=0,
解得:n2=6,或n2=-$\frac{3}{2}$(舍去).
∵n>0,
∴n=$\sqrt{6}$,
∴点P的坐标为($\sqrt{6}$,$\frac{\sqrt{6}}{2}$).
点评 本题考查了反比例函数与一次函数的交点问题、三角形的面积公式、角的计算以及解一元高次方程,解题的关键是通过两种方法求面积找出关于点P横坐标的一元四次方程.本题属于中档题,难度不大,解决该题型题目时,利用切割法以及直接求面积法分别表示出三角形的面积,根据面积相等得出关于点的横坐标的一元高次方程是关键.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了了解某校学生安全知识的掌握情况,随机抽查了部分学生进行10道题安全知识的问答测试,得到如图的条形图,观察该图,可知抽查的学生中全部答对的有多少人?并估算出该校每位学生平均答对几题?(结果精确到0.1)
为了了解某校学生安全知识的掌握情况,随机抽查了部分学生进行10道题安全知识的问答测试,得到如图的条形图,观察该图,可知抽查的学生中全部答对的有多少人?并估算出该校每位学生平均答对几题?(结果精确到0.1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠1,∠2,∠3,∠4,∠5这五个角中哪些是同位角?哪些是内错角?哪些是同旁内角?指出它们分别是哪两条直线被哪一条直线所截形成的角.
如图,∠1,∠2,∠3,∠4,∠5这五个角中哪些是同位角?哪些是内错角?哪些是同旁内角?指出它们分别是哪两条直线被哪一条直线所截形成的角.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com