
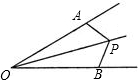
 如图,P为∠AOB内一点,OA=OB,且△OPA与△OPB面积相等,求证:∠AOP=∠BOP.
如图,P为∠AOB内一点,OA=OB,且△OPA与△OPB面积相等,求证:∠AOP=∠BOP.  口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
 如图,P为∠AOB内一点,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于M,交OB于 N,若P1P2=8cm,则△PMN的周长是( )cm.
如图,P为∠AOB内一点,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于M,交OB于 N,若P1P2=8cm,则△PMN的周长是( )cm.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,P为∠AOB内的一点,分别作出点P关于OA、OB的对称点P1、P2,连结P1、P2,交OA于M,交OB于N,若P1P2=13cm,求△MNP的周长?
如图,P为∠AOB内的一点,分别作出点P关于OA、OB的对称点P1、P2,连结P1、P2,交OA于M,交OB于N,若P1P2=13cm,求△MNP的周长?查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江湖州第八中学八年级10月月考数学试卷(解析版) 题型:选择题
如图,P为∠AOB内一点, ,
,
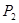 分别是P关于OA、OB的对称点,
分别是P关于OA、OB的对称点,
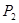 交OA于M,交OB于 N,若
交OA于M,交OB于 N,若
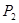 =8㎝,则△PMN的周长是( )㎝
=8㎝,则△PMN的周长是( )㎝
A. 7 B. 5 C. 8 D. 1 0

查看答案和解析>>
科目:初中数学 来源:2012年人教版七年级下第七章角的平分线练习卷(解析版) 题型:解答题
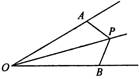
如图,P为∠AOB内一点,OA=OB,且△OPA与△OPB面积相等,求证∠AOP=∠BOP.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com