
 如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,且与BD交于点D;
如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,且与BD交于点D;分析 (1)根据三角形内角和定理和三角形外角的性质即可求得;
(2)根据三角形内角和定理和三角形外角的性质即可求得;
(3)根据三角形内角和定理和三角形外角的性质即可求得;
(4)根据三角形内角和定理以及角平分线性质,先求出∠D、∠A的等式,推出∠D=$\frac{1}{2}$∠A,即可求得结论.
解答 解:(1)∵BD为△ABC的角平分线,∠ABC=60°,
∴∠DBC=30°,
∵∠DCE=70°,
∴∠D=∠DCE-∠DBC=70°-30°=40°;
(2)∵∠ABC=70°,∠A=80°,
∴∠ACE=150°
∵BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,
∴$∠DBC=\frac{1}{2}∠ABC$=35°,∠DCE=$\frac{1}{2}$∠ACE=75°,
∴∠D=∠DCE-∠DBC=75°-35°=40°;
(3)∵∠DCE=∠DBC+∠D,
∴∠D=$\frac{1}{2}$∠ACE-$\frac{1}{2}$∠ABC=$\frac{1}{2}$(∠A+∠ABC)-$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠A,
∵∠ABC+∠ACB=100°,
∴∠A=80°,
∴∠D=40°;
(4)不变化,
理由:∵∠DCE=∠DBC+∠D,
∴∠D=$\frac{1}{2}$∠ACE-$\frac{1}{2}$∠ABC=$\frac{1}{2}$(∠A+∠ABC)-$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠A.
故答案为40;40;40.
点评 此题考查三角形内角和定理以及三角形外角的性质的综合运用,解此题的关键是求出∠D=$\frac{1}{2}$∠A.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:解答题
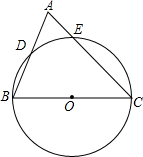 如图所示,△ABC中,BC=4,以BC为直径的半圆交AB于点D,交AC于点E,BD=2,CE=2$\sqrt{2}$.
如图所示,△ABC中,BC=4,以BC为直径的半圆交AB于点D,交AC于点E,BD=2,CE=2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
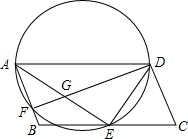 如图,在平行四边形ABCD中,E为BC边上的一点,且AE与DE分别平分∠BAD和∠ADC
如图,在平行四边形ABCD中,E为BC边上的一点,且AE与DE分别平分∠BAD和∠ADC查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,O为AC的中点,EF过O点且EF⊥AC分别交DC于E,交AB于E,点G是AE的中点,且∠AOG=30°,则下列结论:(1)DC=3OG;(2)OG=$\frac{1}{2}$BC;(3)四边形AECF为菱形;(4)S△AOE=$\frac{1}{6}$S四边形ABCD.其中正确的个数为( )
如图,在矩形ABCD中,O为AC的中点,EF过O点且EF⊥AC分别交DC于E,交AB于E,点G是AE的中点,且∠AOG=30°,则下列结论:(1)DC=3OG;(2)OG=$\frac{1}{2}$BC;(3)四边形AECF为菱形;(4)S△AOE=$\frac{1}{6}$S四边形ABCD.其中正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
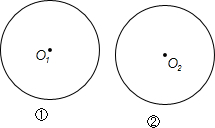 如图,所给两圆的圆心分别为O1,O2,半径都为3,根据要求完成作图(保留作图痕迹,不写作法).
如图,所给两圆的圆心分别为O1,O2,半径都为3,根据要求完成作图(保留作图痕迹,不写作法).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com