
【题目】探索规律:
观察下面由※组成的图案和算式,解答问题:

1+3=4=22
1+3+5=9=32
1+3+5+7=19=42
1+3+5+7+9=25=52
(1)请猜想1+3+5+7+9+ … +19的结果;
(2)请猜想1+3+5+7+9+ … +(2n-1)+(2n+1)+(2n+3)的结果;
(3)请用上述规律计算:51+53+55+…+99+101.
【答案】(1)![]() 或100;(2)
或100;(2)![]() ;(3)1976
;(3)1976
【解析】
根据等式发现:从1开始的连续奇数之和等于奇数个数的平方,从1到19有10个奇数,故结果为10的平方;②由2n+3与1的和除以2计算出奇数的个数,把求出的个数平方即可得到结果.
(1)从1到19的奇数个数为![]() =10个,
=10个,
∴1+3+5+7+9+…+19=102;
(2)从1到2n+3的奇数个数为:![]() =n+2,
=n+2,
∴1+3+5+7+9+…+(2n1)+(2n+1)+(2n+3)=(n+2)2;
(3)51+53+55+…+99+101=1+3+5+7+9+…+101-(1+3+5+7+9+…49)
=512-252=1976;
故答案为:102;n+2;1976.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线y= ![]() x与双曲线y=
x与双曲线y= ![]() (k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y=
(k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y= ![]() (k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为( )
(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为( ) 
A.(2,4)
B.(1,8)
C.(2,4)或(1,8)
D.(2,4)或(8,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标). 
(1)求P点落在正方形ABCD面上(含正方形内部和边界)的概率.
(2)将正方形ABCD平移整数个单位,则是否存在一种平移,使点P落在正方形ABCD 面上的概率为 ![]() ;若存在,指出其中的一种平移方式;若不存在,请说明理由.
;若存在,指出其中的一种平移方式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将5个完全相同的小球分装在甲、乙两个不透明的口袋中.甲袋中有3个球,分别标有数字2,3,4;乙袋中有2个球,分别标有数字2,4.从甲、乙两个口袋中各随机摸出一个球.
(1)用列表法或画树状图法,求摸出的两个球上数字之和为5的概率.
(2)摸出的两个球上数字之和为多少时的概率最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
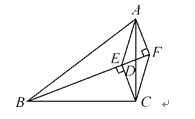
【题目】如图所示,BD是△ABC的中线,CE⊥BD于点E,AF⊥BD,交BD的延长线于点F.
(1)试探索BE,BF和BD三者之间的数量关系,并加以证明;
(2)连接AE,CF,求证:AE∥CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】煤气公司一工人检修一条长540米的煤气管道,计划用若干小时完成,在实际检修过程中,每小时检修的管道长度是原计划的1.5倍,结果提前3小时完成任务,求该工人原计划每小时检修煤气管道多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣20+8﹣(﹣1)+(﹣4)
(2)![]() ×(﹣
×(﹣![]() )2÷(﹣0.5)3
)2÷(﹣0.5)3
(3)4﹣6÷(﹣2)×(﹣![]() )
)
(4)(﹣36)×(﹣![]() +
+![]() ﹣
﹣![]() )
)
(5)(﹣2)2×0.5﹣(﹣1.6)2÷(﹣2)3
(6)﹣14÷(﹣4)﹣(﹣![]() )2×(﹣3)+|(﹣1)2﹣2|
)2×(﹣3)+|(﹣1)2﹣2|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com