
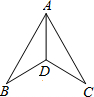
 如图,已知∠BAD=∠CAD,图中再补充一个条件后不能说明△ABD≌△ACD,则这个条件是( )
如图,已知∠BAD=∠CAD,图中再补充一个条件后不能说明△ABD≌△ACD,则这个条件是( )| A. | AB=AC | B. | ∠B=∠C | C. | BD=CD | D. | ∠ADB=∠ADC |
分析 要判定△ABD≌△ACD,已有条件∠BAD=∠CAD,公共边AD=AD,再根据所给选项结合判定方法进行分析即可.
解答 解:A、补充AB=AC可利用SAS判定△ABD≌△ACD,故此选项不合题意;
B、补充∠B=∠C可利用AAS判定△ABD≌△ACD,故此选项不合题意;
C、补充BD=DC不能判定△ABD≌△ACD,故此选项符合题意;
D、补充∠ADB=∠ADC可利用ASA判定△ABD≌△ACD,故此选项不合题意;
故选:C.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


科目:初中数学 来源: 题型:解答题
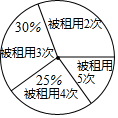 宜昌市城区公共自行车于2017年2月22日起试运行,市民租用公共自行车的收费标准为:1小时内免费,达到并超过1小时收费1元,达到并超过2小时收费2元,达到并超过3小时收费3元…
宜昌市城区公共自行车于2017年2月22日起试运行,市民租用公共自行车的收费标准为:1小时内免费,达到并超过1小时收费1元,达到并超过2小时收费2元,达到并超过3小时收费3元…| 被租用的次数 | 2 | 3 | 4 | 5 |
| 被租用的辆数 | x | a | 5 | y |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
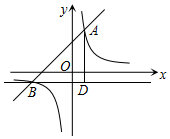 如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(1,3)和B(-3,m).
如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(1,3)和B(-3,m).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
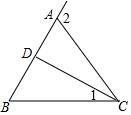 已知∠2是△ABC的一个外角,那么∠2与∠B+∠1的大小关系是( )
已知∠2是△ABC的一个外角,那么∠2与∠B+∠1的大小关系是( )| A. | ∠2>∠B+∠1 | B. | ∠2=∠B+∠1 | C. | ∠2<∠B+∠1 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
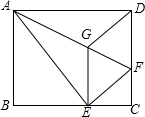 如图所示,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
如图所示,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
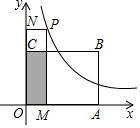 如图,矩形OABC的四个顶点分别为O(0,0),A(2,0),B(2,1),C(0,1),P(x,y)是反比例函数y=$\frac{1}{x}$(x>0)图象上的一个动点,过点P作PM⊥x轴,PN⊥y轴,M、N为垂足,记矩形OMPN与矩形OABC的重叠部分面积为S,则S与x轴的函数关系式的图象为( )
如图,矩形OABC的四个顶点分别为O(0,0),A(2,0),B(2,1),C(0,1),P(x,y)是反比例函数y=$\frac{1}{x}$(x>0)图象上的一个动点,过点P作PM⊥x轴,PN⊥y轴,M、N为垂足,记矩形OMPN与矩形OABC的重叠部分面积为S,则S与x轴的函数关系式的图象为( )| A. | 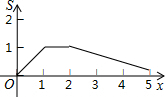 | B. | 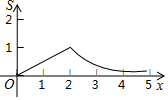 | ||
| C. | 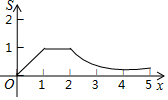 | D. | 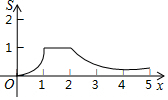 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
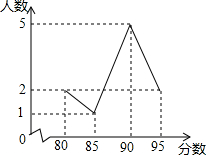 在学校演讲比赛中,10名选手的成绩折线统计图如图所示,则下列说法正确的是( )
在学校演讲比赛中,10名选手的成绩折线统计图如图所示,则下列说法正确的是( )| A. | 最高分90 | B. | 众数是5 | C. | 中位数是90 | D. | 平均分为87.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com