
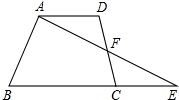
 四边形ABCD中,AD∥BC,DF=CF,连接AF并延长交BC延长线于点E.
四边形ABCD中,AD∥BC,DF=CF,连接AF并延长交BC延长线于点E.| 1 |
| 2 |


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
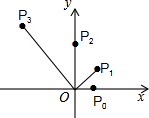 如图,在平面直角坐标系中,已知点P0的坐标为(1,0)将线段OP按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1,又将线段OP1按逆时针方向旋转45°,再将其长度伸长为OP1的2倍得到线段OP2;…;如此进行下去,得到线段OP3,OP4,…OPn(n为正整数)则点P2015的坐标为( )
如图,在平面直角坐标系中,已知点P0的坐标为(1,0)将线段OP按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1,又将线段OP1按逆时针方向旋转45°,再将其长度伸长为OP1的2倍得到线段OP2;…;如此进行下去,得到线段OP3,OP4,…OPn(n为正整数)则点P2015的坐标为( )A、(22014•
| ||||
B、(22012•
| ||||
C、(-22013•
| ||||
| D、(0,-22014) |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、y1<y2<y3 |
| B、y3<y2<y1 |
| C、y2<y1<y3 |
| D、y2<y3<y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
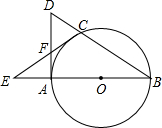 如图,AB是⊙O的直径,C是⊙O上的一点,过点A作DA⊥BA于点A,交BC的延长线于点D,延长BA至点E,连接CE交DA于点F,恰使AF=DF
如图,AB是⊙O的直径,C是⊙O上的一点,过点A作DA⊥BA于点A,交BC的延长线于点D,延长BA至点E,连接CE交DA于点F,恰使AF=DF查看答案和解析>>
科目:初中数学 来源: 题型:
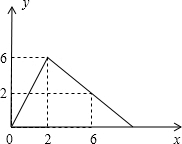 某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,当成人按规定服药后:
某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,当成人按规定服药后:查看答案和解析>>
科目:初中数学 来源: 题型:
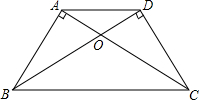 如图,AB⊥AC,DC⊥DB,填空:
如图,AB⊥AC,DC⊥DB,填空:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com