
����Ŀ����ͼ����֪������![]() ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��
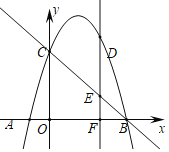
��1��ֱ��д����A��B��C�����ꣻ
��2���������ߵĶԳ����ϴ���һ��P��ʹ��PA+PC��ֵ��С�����ʱ��P�����ꣻ
��3����D�ǵ�һ�������������ϵ�һ�����㣨���C��B���غϣ�����D��DF��x���ڵ�F����ֱ��BC�ڵ�E������BD��ֱ��BC����BDF������ֳ������֣�ʹ![]() ���������D�����ꣻ
���������D�����ꣻ
��4����MΪ�����߶Գ�����һ���㣬ʹ����MBCΪֱ�������Σ���ֱ��д����M�����꣮
���𰸡���1����A��B��C������ֱ�Ϊ����1��0������5��0������0��5������2��P��2��3������3��D��![]() ��
��![]() ������4��M����������2��7����2��3����2��6����2��1����
������4��M����������2��7����2��3����2��6����2��1����
��������
��1����y��0����x��1��5����x��0����y��5��������⣻
��2����B�ǵ�A���ں����Գ���ĶԳƵ㣬����BC�������߶Գ����ڵ�P�����PΪ��������⣻
��3��S��BDE��S��BEF��2��3����![]() ������
������![]() ��������⣻
��������⣻
��4����MBΪб�ߡ�MCΪб�ߡ�BCΪб������������ֱ���⼴�ɣ�
��1����y��0����x��1��5����x��0����y��5��
�ʵ�A��B��C������ֱ�Ϊ����1��0������5��0������0��5����
��2�������ߵĶԳ���Ϊ��x��2��
��B�ǵ�A���ں����Գ���ĶԳƵ㣬����BC�������߶Գ����ڵ�P�����PΪ����
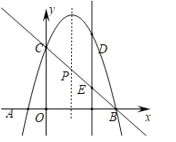
ֱ��BC�ı���ʽΪ��y��x��5��
��x��2ʱ��y��3���ʵ�P��2��3����
��3�����D��x��x2��4x��5�������E��x��x��5����
��S��BDE��S��BEF��2��3����![]() ��
��
����![]() ��
��
��ã�m��![]() ��5����ȥ5����
��5����ȥ5����
�ʵ�D��![]() ��
��![]() ����
����
��4�����M��2��m��������B��C������ֱ�Ϊ����5��0������0��5����
��MB2��9��m2��MC2��4����m5��2��BC2��50��
�ٵ�MBΪб��ʱ����9��m2��4����m5��2��50����ã�m��7��
�ڵ�MCΪб��ʱ����4����m5��2=9��m2+50���ɵã�m��3��
�۵�BCΪб��ʱ����4����m5��2+9��m2=50�ɵã�m��6��1��
���ϵ�M������Ϊ����2��7����2��3����2��6����2��1����


 �����ߴ���ϵ�д�
�����ߴ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһƽ��ֱ������ϵ�У�����y��ax2+bx��y����bx+a��ͼ������ǣ�������
A. B.
B. C.
C.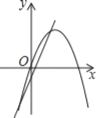 D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
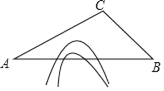
����Ŀ�������й����õĿ��ٷ�չ�Լ��Ƽ�ˮƽ�ķ�����ߣ��й�������Ѹ�����𣮸������������ʱ�վ��룬�ı������ǵij��з�ʽ����ͼ��A��B���ر���ɽ�������A�ص�B����Ҫ����C�أ�����ͨ��ɽ����������A��B���ص�ֱ��������������̴�A�ص�B�ص�·�̣���֪����CAB=30�㣬��CBA=45�㣬AC=640�����������ͨ�����ͨǰ��ȣ���A�ص�B�ص�·�̽�Լ���̶��ٹ�����ο����ݣ�![]() ��1.7��
��1.7��![]() ��1.4��
��1.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��ͼ�����㣨1��0������-3��0������0��
��ͼ�����㣨1��0������-3��0������0��![]() ��.
��.
��1����ö��κ����Ľ���ʽ��
��2��������������![]() ͼ������κ���
ͼ������κ���![]() ��ͼ���ڵ�һ�����ڽ��ڵ�
��ͼ���ڵ�һ�����ڽ��ڵ�![]() ,
, ![]() �����������ڵ�������֮�䣬��д�����������ڵ���������
�����������ڵ�������֮�䣬��д�����������ڵ���������
��3��������������![]() ��ͼ������κ���
��ͼ������κ���![]() ��ͼ���ڵ�һ�����ڵĽ���ΪA����A�ĺ�����Ϊ
��ͼ���ڵ�һ�����ڵĽ���ΪA����A�ĺ�����Ϊ![]() ����
����![]() ������ʵ��
������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���![]() ͼ����ͼ��ʾ�����н��ۣ���
ͼ����ͼ��ʾ�����н��ۣ���![]() ����
����![]() ���۵�
���۵�![]() ʱ��
ʱ��![]() ����
����![]() ������
������![]() ����
����![]() ����
����![]() ��������ȷ����______.
��������ȷ����______.
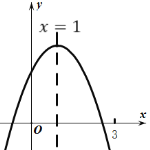
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У���E��BC���е㣬����DE������A��AG��ED��DE�ڵ�F����CD�ڵ�G��
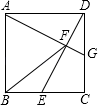
��1��֤������ADG�ա�DCE����2������BF��֤����AB��FB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=3cm��BC=6cm.��P�ӵ�D�������A�˶����˶�����A��ֹͣ��ͬʱ����Q�ӵ�B�������C�˶����˶�����C��ֹͣ����P��Q���ٶȶ���1cm/s.����PQ��AQ��CP.���P��Q�˶���ʱ��Ϊts.
��tΪ��ֵʱ���ı���ABQP�Ǿ��Σ�
��tΪ��ֵʱ���ı���AQCP�����Σ�
�ֱ������2��������AQCP���ܳ������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
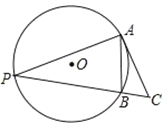
����Ŀ����ͼ��O�İ뾶Ϊ1����AB��1����PΪ�Ż�AB��һ���㣬AC��AP��ֱ��PB�ڵ�C������ABC���������ǣ��� ����
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һԪ���η���![]() �У���ϵ��
�У���ϵ��![]() ��
��![]() ����0��1��2��3��ȡֵ����������ʵ����ķ��̵ĸ�����___ ����д���������������ʵ������һԪ���η���_________.
����0��1��2��3��ȡֵ����������ʵ����ķ��̵ĸ�����___ ����д���������������ʵ������һԪ���η���_________.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com