
分析 根据根与系数关系得到α+β=$\frac{m}{2}$,αβ=-$\frac{3}{2}$,然后可以得到α2β+αβ2-αβ=-$\frac{3}{2}$($\frac{m}{2}$-1)≥0,从而解不等式即可得到答案.
解答 解:∵α,β是关于x的一元二次方程2x2-mx-3=0的两个实根,
∴α+β=$\frac{m}{2}$,αβ=-$\frac{3}{2}$,
∴α2β+αβ2-αβ=αβ(α+β-1)=-$\frac{3}{2}$($\frac{m}{2}$-1)≥0,
∴m-2≤0,
∴m≤2,
故答案为:m≤2.
点评 本题主要考查了根与系数关系,解题的关键是把α2β+αβ2-αβ转化为αβ(α+β-1)的形式,此题难度不大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
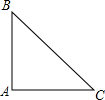 在△ABC中,∠BAC=90°,AB=AC=4,在△ABC的外部,以AB为直角边作等腰直角△ABD,连接CD,则△BCD的周长为4$\sqrt{5}$+4$\sqrt{2}$+4或8$\sqrt{2}$+8.
在△ABC中,∠BAC=90°,AB=AC=4,在△ABC的外部,以AB为直角边作等腰直角△ABD,连接CD,则△BCD的周长为4$\sqrt{5}$+4$\sqrt{2}$+4或8$\sqrt{2}$+8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
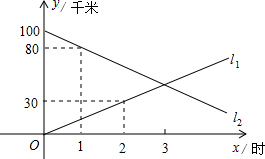 A、B两地相距100千米,甲、乙两人骑车同时分别从A,B两地出发,相向而行.假设他们都保持匀速行驶,则他们各自离A地的距离y(千米)都是骑车时间x(时)的一次函数,1小时后乙距离A地80千米;2时后甲距离A地30千米.
A、B两地相距100千米,甲、乙两人骑车同时分别从A,B两地出发,相向而行.假设他们都保持匀速行驶,则他们各自离A地的距离y(千米)都是骑车时间x(时)的一次函数,1小时后乙距离A地80千米;2时后甲距离A地30千米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
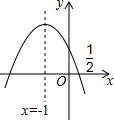 如图,抛物线y=ax2+bx+c(a≠0)的对称轴是x=-1,且过点($\frac{1}{2}$,0),有下列结论:①abc>0;②a-2b+4c=0;③25a-10b+4c=0;④3b+2c>0.其中所有正确的结论是①③(填写序号)
如图,抛物线y=ax2+bx+c(a≠0)的对称轴是x=-1,且过点($\frac{1}{2}$,0),有下列结论:①abc>0;②a-2b+4c=0;③25a-10b+4c=0;④3b+2c>0.其中所有正确的结论是①③(填写序号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com