
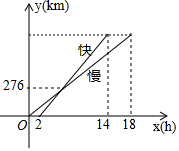
 如图是一辆慢车与一辆快车沿相同路线从A地到B地所行的路程与时间之间的函数图象,已知慢车比快车早出发2小时,则A、B两地的距离为828 km.
如图是一辆慢车与一辆快车沿相同路线从A地到B地所行的路程与时间之间的函数图象,已知慢车比快车早出发2小时,则A、B两地的距离为828 km. 分析 根据数量关系“路程=速度×时间”结合函数图象,即可得出v快=$\frac{3}{2}$v慢,设两车相遇的时间为t,根据数量关系“路程=速度×时间”即可得出t•v慢=(t-2)•v快=276,解之即可得出t与v慢的值,将慢车的速度代入s=18v慢中即可求出A、B两地的距离.
解答 解:根据函数图象可知:s=(14-2)v快=18v慢,
∴v快=$\frac{3}{2}$v慢.
设两车相遇的时间为t,
根据函数图象可知:t•v慢=(t-2)•v快=276,
解得:t=6,v慢=46,
∴s=18v慢=18×46=828.
故答案为:828.
点评 本题考查了函数的图象以及解一元一次方程,根据数量关系结合函数图象找出快、慢两车速度间的关系是解题的关键.


科目:初中数学 来源: 题型:解答题
 在压力不变的情况下,某物体所承受的压强P(pa)与它的受力面积S(m2)之间的函数关系如图所示.
在压力不变的情况下,某物体所承受的压强P(pa)与它的受力面积S(m2)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
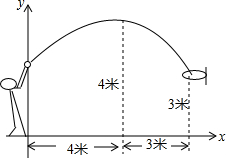 如图示:学校九年级的一场篮球比赛中,队员甲正在投篮,已知球出手时离地面高为$\frac{20}{9}$米,与篮筐中心的水平距离为7米,当球出手后球与队员甲的水平距离为4米时球达到最大高度4米,设篮球运行的轨迹为抛物线,篮筐距地面3米.
如图示:学校九年级的一场篮球比赛中,队员甲正在投篮,已知球出手时离地面高为$\frac{20}{9}$米,与篮筐中心的水平距离为7米,当球出手后球与队员甲的水平距离为4米时球达到最大高度4米,设篮球运行的轨迹为抛物线,篮筐距地面3米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
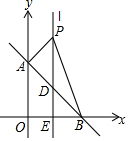 如图,平面直角坐标系中,直线AB:y=-x+b交y轴于点A(0,4),交x轴于点B.
如图,平面直角坐标系中,直线AB:y=-x+b交y轴于点A(0,4),交x轴于点B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
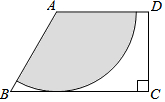 如图,梯形ABCD中,AD∥BC,∠C=90°,∠B=60°,AB=4,以点A为圆心在这个梯形内画出一个最大的扇形(图中阴影部分),则这个扇形的面积是4π.
如图,梯形ABCD中,AD∥BC,∠C=90°,∠B=60°,AB=4,以点A为圆心在这个梯形内画出一个最大的扇形(图中阴影部分),则这个扇形的面积是4π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com