

 解:将N点向左平移2单位与P重合,点B向左平移2单位到B′(2,-1),
解:将N点向左平移2单位与P重合,点B向左平移2单位到B′(2,-1),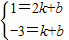 ,解得k=4,b=-7.
,解得k=4,b=-7. ,即P(
,即P( ,0),a=
,0),a= .
. .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(广西钦州卷)数学 题型:解答题
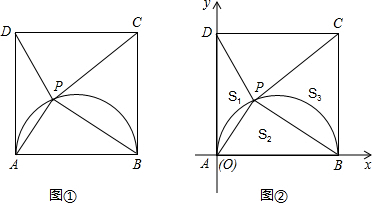
(本题满分8分)已知四边形ABCD是边长为4的正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PB、PC、PD.
(1)如图①,当PA的长度等于
时,∠PAB=60°;
当PA的长度等于 时,△PAD是等腰三角形;
(2)如图②,以AB边所在直线为x轴、AD边所在直线为y轴,建立如图所示的直角
坐标系(点A即为原点O),把△PAD、△PAB、△PBC的面积分别记为S1、S2、S3.坐
标为(a,b),试求2 S1 S3-S22的最大值,并求出此时a,b的值.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市密云九年级上学期期末考试数学试卷(解析版) 题型:解答题
已知四边形ABCD是边长为4的正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PB、PC、PD.
(1)如图①,当PA的长度等于 时,∠PAB=60°;当PA的长度等于 时,△PAD是等腰三角形;
(2)如图②,以AB边所在直线为x轴、AD边所在直线为y轴,建立如图所示的直角坐标系(点A即为原点O),把△PAD、△PAB、△PBC的面积分别记为S1、S2、S3.坐标为(a,b),试求2 S1 S3-S22的最大值,并求出此时a,b的值.

查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(广西钦州卷)数学 题型:解答题
(本题满分8分)已知四边形ABCD是边长为4的正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PB、PC、PD.
(1)如图①,当PA的长度等于
时,∠PAB=60°;
当PA的长度等于 时,△PAD是等腰三角形;
(2)如图②,以AB边所在直线为x轴、AD边所在直线为y轴,建立如图所示的直角
坐标系(点A即为原点O),把△PAD、△PAB、△PBC的面积分别记为S1、S2、S3.坐
标为(a,b),试求2 S1 S3-S22的最大值,并求出此时a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com