练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】用如图所示的曲尺形框框（有三个方向），可以套住下表中的三个数，设被框住的三个数中最小的数为a.

    ⑴用含a的式子表示这三个数的和；

    ⑵若这三个数的和是48，求a的值.

    【答案】（1）第一个框的和为3a+8，第二个框的和为3a+15，第三个框的和为3a+9；（2）11或13

    【解析】

    （1）注意三种不同的框圈住的三个数之间的大小关系，要分三种情况进行分析；
    （2）根据三种不同的结果列方程求解，求得的数必须是整数，否则应舍去．

    ⑴设被第一个框框住的三个数中最小的数为a,则

    a+a+1+a+7=3a+8，

    设被第二个框框住的三个数中最小的数为a,则

    a+a+7+a+8=3a+15，

    设被第三个框框住的三个数中最小的数为a,则

    a+a+1+a+8=3a+9；

    ⑵设被第一个框框住的三个数的和是48，则

    3a+8=48，解得.显然和题意不合.

    设被第二个框框住的三个数的和是48，则

    3a+15=48，解得.符合题意.

    设被第三个框框住的三个数的和是48，则

    3a+9=48，解得.符合题意.

    ∴a的值为11或13.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（1）计算下列各题：

    ①2x2﹣4x+1+2x﹣5x2

    ②（8x﹣3x2）﹣5xy﹣2（3xy﹣2x2）

    （2）先化简，再求值：（3x2y+5x）﹣[x2y﹣4（x﹣x2y）]，其中（x+2）2+|y﹣3|=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系内，直线l⊥y轴于点C(C在y轴的正半轴上)，与直线y=相交于点A，和双曲线y=交于点B，且AB=6，则点B的坐标是______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，锐角△ABC内接于⊙O，若⊙O的半径为6，sinA=，求BC的长．

    【答案】BC=8．

    【解析】试题分析：通过作辅助线构成直角三角形，再利用三角函数知识进行求解．

    试题解析：作⊙O的直径CD，连接BD，则CD=2×6=12.

    ∵

    ∴

    ∴

    点睛：直径所对的圆周角是直角.

    【题型】解答题
    【结束】
    22

    【题目】如图，一次函数y=k1x+b与反比例函数y=的图象交于A（2，m），B（n，﹣2）两点．过点B作BC⊥x轴，垂足为C，且S△ABC=5．

    （1）求一次函数与反比例函数的解析式；

    （2）根据所给条件，请直接写出不等式k1x+b＞的解集；

    （3）若P（p，y1），Q（﹣2，y2）是函数y=图象上的两点，且y1≥y2，求实数p的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在我市中小学生“我的中国梦”读书活动中，某校对部分学生做了一次主题为“我最喜爱的图书”的调查活动，将图书分为甲、乙、丙、丁四类，学生可根据自己的爱好任选其中一类。学校根据调查情况进行了统计，并绘制了不完整的条形统计图和扇形统计图。

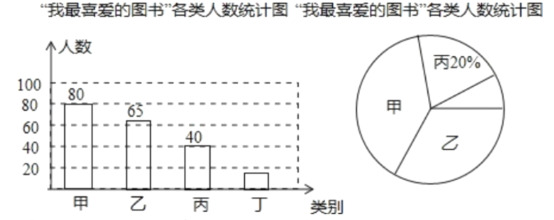
    请你结合图中信息，解答下列问题：

    (1)本次共调查了___名学生；

    (2)被调查的学生中，最喜爱丁类图书的有___人，最喜爱甲类图书的人数占本次被调查人数的___%；

    (3)在最喜爱丙类学生的图书的学生中，女生人数是男生人数的1.5倍，若这所学校共有学生1500人，请你估计该校最喜爱丙类图书的女生和男生分别有多少人。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知点D、E分别在△ABC的边AC、BC上，线段BD与AE交于点F，且CDCA=CECB．

    （1）求证：∠CAE=∠CBD；

    （2）若，求证：ABAD=AFAE．

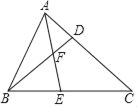
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,BD是△ABC的角平分线,点E,F分别在BC、AB上,且DE∥AB,EF∥AC.

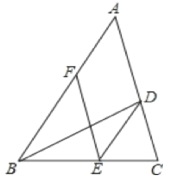
    (1)求证：BE=AF；

    (2)若∠ABC=60°，BD=6，求四边形ADEF的面积。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角梯形ABCD中，AB∥DC，∠D=90°，AC⊥BC，AB=10cm，BC=6cm，F点以2cm/秒的速度在线段AB上由A向B匀速运动，E点同时以1cm/秒的速度在线段BC上由B向C匀速运动，设运动时间为t秒（0＜t＜5）．

    （1）求证：△ACD∽△BAC；

    （2）求DC的长；

    （3）设四边形AFEC的面积为y，求y关于t的函数关系式，并求出y的最小值．

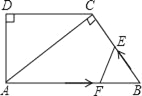
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个自然数的立方，可以分裂成若干个连续奇数的和．例如：23，33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和，即23=3+5；33=7+9+11；43=13+15+17+19；…；若103也按照此规律来进行“分裂”，则103“分裂”出的奇数中，最小的奇数是_________

    查看答案和解析>>

    同步练习册答案