
【题目】某学校要从甲乙两名射击运动员中挑选一人参加全市比赛,在选拔赛中,每人进行了5次射击,甲的成绩(环)为:9.7,10,9.6,9.8,9.9;乙的成绩的平均数为9.8,方差为0.032;
(1)甲的射击成绩的平均数和方差分别是多少?
(2)据估计,如果成绩的平均数达到9.8环就可能夺得金牌,为了夺得金牌,应选谁参加比赛?
科目:初中数学 来源: 题型:
【题目】如图6,在平面直角坐标系中,一次函数![]() =
=![]() +1的图象交
+1的图象交![]() 轴于点D,与反比例函数
轴于点D,与反比例函数![]() =
=![]() 的图象在第一象限相交于点A.过点A分别作
的图象在第一象限相交于点A.过点A分别作![]() 轴
轴![]() 轴的垂线,垂足为点BC.
轴的垂线,垂足为点BC.
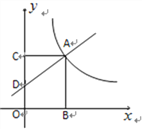
(1)点D的坐标为 ;
(2)当AB=4AC时,求![]() 值;
值;
(3)当四边形OBAC是正方形时,直接写出四边形ABOD与△ACD面积的比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市水果批发部门欲将 A 市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为 200 元/ 时.其它主要参考数据如下:
运输工具 | 途中平均速度(千米/ 时) | 运费(元/ 千米) | 装卸费用(元) |
火车 | 100 | 15 | 2000 |
汽车 | 80 | 20 | 900 |
运输过程中,火车因多次临时停车,全程在路上耽误 2 小时 45 分钟,火车的总支出费用与汽车的总支出费用相同,请问某市与本地的路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,抛物线![]() 与x轴相交于点A,B,与y轴相交于点C. 已知A,C两点的坐标分别为A(-4,0), C(0,4).
与x轴相交于点A,B,与y轴相交于点C. 已知A,C两点的坐标分别为A(-4,0), C(0,4).
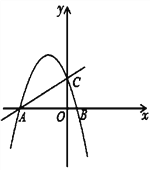
(1)求抛物线的表达式;
(2)如果点P,Q在抛物线上(P点在对称轴左边),且PQ∥AO,PQ=2AO,求P,Q的坐标;
(3)动点M在直线y=x+4上,且△ABC与△COM相似,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
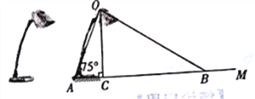
【题目】图为放置在水平桌面上的台灯的平面示意图,可伸缩式灯臂AO长为40 cm,与水平面所形成的夹角∠OAM恒为75°(不受灯臂伸缩的影响).由光源0射出的光线沿灯罩形成光线OC,OB,与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°.
(1)求该台灯照亮桌面的宽度BC.(不考虑其他因素,结果精确到1 cm,参考数据:sin75°≈0.97,cos75°≈0.26, ![]() ≈1.73)
≈1.73)
(2)若灯臂最多可伸长至60 cm,不调整灯罩的角度,能否让台灯照亮桌面85 cm的宽度?
查看答案和解析>>
科目:初中数学 来源: 题型:
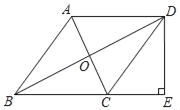
【题目】如图,O为△ABC边AC的中点,AD∥BC交BO的延长线于点D,连接DC,DB平分∠ADC,作DE⊥BC,垂足为E.
(1)求证:四边形ABCD为菱形;
(2)若BD=8,AC=6,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是几何学中的明珠,充满着魅力,千百年来,人们对它趋之若鹜,其中有著名的数学家,也有业余数学爱好者,向常春在1994年构造发现了一个新的证法:把两个全等的直角三角形如图1放置,其三边长分别为a、b、c,显然∠DAB=∠B=90°,AC⊥DE.
(1)请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再通过探究这三个图形面积之间的关系,证明:勾股定理a2+b2=c2;
(2)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=24千米,BC=16千米,在AB上有一个供应站P,且PC=PD,求出AP的距离;
(3)借助(2)的思考过程与几何模型,直接写出代数式![]() 的最小值为 .
的最小值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠CAB=30°,BC=2,O、H分别为边AB、AC的中点,将△ABC绕点B顺时针旋转120°到△A1BC1的位置,则整个旋转过程中线段OH所扫过部分的面积(即阴影部分面积)为_____.
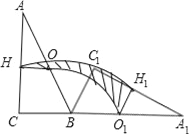
查看答案和解析>>
科目:初中数学 来源: 题型:
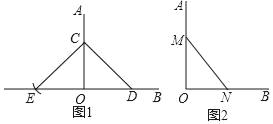
【题目】“直角”在初中数学学习中无处不在在数学活动课上,李老师要求同学们用所学知识,利用无刻度的直尺和圆规判断“已知∠AOB“是不是直角.甲、乙两名同学各自给出不同的作法,来判断∠AOB是不是直角
甲:如图1,在OA、OB上分别取点CD,以C为圆心,CD长为半径画弧,交OB的反向延长线于点E,若OE=OD,则∠AOB=90°;
乙:如图2,在OA、OB上分别截取OM=4个单位长度,ON=3个单位长度,若MN=5个单位长度,则∠AOB=90°;
甲、乙两位同学作法正确的是( )
A. 甲正确,乙不正确B. 乙正确,甲不正确
C. 甲和乙都不正确D. 甲和乙都正确
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com