
【题目】如图,点C是⊙O上一点,⊙O的半径为 ![]() ,D、E分别是弦AC、BC上一动点,且OD=OE=
,D、E分别是弦AC、BC上一动点,且OD=OE= ![]() ,则AB的最大值为( )
,则AB的最大值为( ) 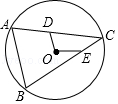
A.![]()
B.![]()
C.![]()
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了倡导“节约用水,从我做起”,南沙区政府决定对区直属机关300户家庭的用水情况作一次调查,区政府调查小组随机抽查了其中50户家庭一年的月平均用水量(单位:吨),调查中发现每户用水量均在10﹣14吨/月范围,并将调查结果制成了如图所示的条形统计图.

(1)请将条形统计图补充完整;
(2)这50户家庭月用水量的平均数是 ,众数是 ,中位数是 ;
(3)根据样本数据,估计南沙区直属机关300户家庭中月平均用水量不超过12吨的约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个含45°角的直角三角板BEF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点B重合,联结DF,点M,N分别为DF,EF的中点,联结MA,MN.
(1)如图1,点E,F分别在正方形的边CB,AB上,请判断MA,MN的数量关系和位置关系,直接
写出结论;
(2)如图2,点E,F分别在正方形的边CB,AB的延长线上,其他条件不变,那么你在(1)中得到的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.


图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA为⊙O的切线,A为切点,过A作OP的垂线AB,垂足为点C,交⊙O于点B,延长BO与⊙O交于点D,与PA的延长线交于点E. 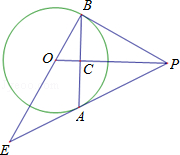
(1)求证:PB为⊙O的切线;
(2)若tan∠ABE= ![]() ,求sin∠E.
,求sin∠E.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】∠AOB与∠COD有共同的顶点O,其中∠AOB=∠COD=60°.
(1)如图①,试判断∠AOC与∠BOD的大小关系,并说明理由;
(2)如图①,若∠BOC=10°,求∠AOD的度数;
(3)如图①,猜想∠AOD与∠BOC的数量关系,并说明理由;
(4)若改变∠AOB,∠COD的位置,如图②,则(3)的结论还成立吗?若成立,请证明;若不成立,请直接写出你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A=∠B=90°,E是AB上一点,且AE=BC,∠1=∠2.
(1)证明:AB=AD+BC;
(2)判断△CDE的形状?并说明理由.
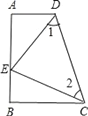
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学在实施快乐大课间之前组织过“我最喜欢的球类”的调查活动,每个学生仅选择一项,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制成的不完整统计图. 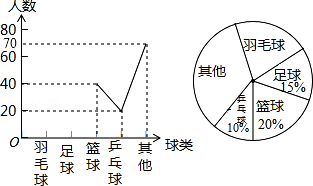
(1)求出被调查的学生人数;
(2)把折线统计图补充完整;
(3)小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.如果确定小亮打第一场,其余三人用“手心、手背”的方法确定谁获胜谁打第一场若三人中有一人出的与其余两人不同则获胜;若三人出的都相同则平局.已知大刚出手心,请用树状图分析大刚获胜的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知方程:①3x﹣1=2x+1,②![]() ,③
,③![]() ,④
,④![]() x﹣1=x中,解为x=2的是方程( )
x﹣1=x中,解为x=2的是方程( )
A. ①、②和③ B. ①、③和④ C. ②、③和④ D. ①、②和④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com