
【题目】我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.
(1)如图,在![]() 中,点
中,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,设
上,设![]() ,
,![]() 相交于点
相交于点![]() ,若
,若![]() ,
,![]() .请你写出图中一个与
.请你写出图中一个与![]() 相等的角,并猜想图中哪个四边形是等对边四边形?
相等的角,并猜想图中哪个四边形是等对边四边形?
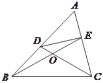
(2)在![]() 中,如果
中,如果![]() 是不等于
是不等于![]() 的锐角,点
的锐角,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,且
上,且![]() .探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
【答案】(1)与∠A相等的角是∠BOD、∠COE,四边形DBCE是等对边四边形;(2)存在等对边四边形DBCE,证明见解析;
【解析】
(1)根据三角形外角的性质可得∠BOD=60°,根据对顶角的性质可得∠COE=60°;作CG⊥BE于G点,作BF⊥C,D交CD延长线于F点通过证明△BCF≌△CBG,可得BF=CG,,再证明△BDF≌△CEG,即可证明四边形DBCE是等对边四边形;
(2)作CG⊥BE于G点,作BF⊥CD交CD延长线于F点.易证△BCF≌△CBG,进而证明△BDF≌△CEG,所以BD=CE,所以四边形DBCE是等对边四边形.
(1)∵∠A=60°,![]()
∴∠OBC=∠OCB=30°
∴∠BOD=∠COE=∠OBC+∠OCB=30°+30°=60°,
∴与∠A相等的角是∠BOD、∠COE,
四边形DBCE是等对边四边形,证明如下:
如图,作CG⊥BE于G点,作BF⊥CD交CD延长线于F点.
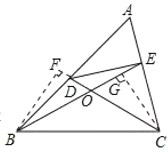
∴∠BFC=∠CGB=∠CGE=90°
∵∠DCB=∠EBC=![]() ∠A,BC=BC,
∠A,BC=BC,
∴△BCF≌△CBG,
∴BF=CG,
∵∠BDF=∠ABE+∠DOB,∠BEC=∠ABE+∠A,∠A=∠BOD
∴∠BDF=∠BEC,
又∵∠BFD=∠CGE=90°,BF=CG,
∴△BDF≌△CEG,
∴BD=CE,
∴四边形DBCE是等对边四边形.
(2)存在等对边四边形DBCE,理由如下:
如图,作CG⊥BE于G点,作BF⊥CD交CD延长线于F点.

∴∠BFC=∠CGB=∠CGE=90°
∵∠DCB=∠EBC=![]() ∠A,BC=BC,
∠A,BC=BC,
∴△BCF≌△CBG,
∴BF=CG,
∵![]()
∴∠BOD =∠OBC+∠OCB=![]() ,
,
∴∠A=∠BOD,
∵∠BDF=∠ABE+∠DOB,∠BEC=∠ABE+∠A,
∴∠BDF=∠BEC,
又∵∠BDF=∠CGE=90°,BF=CG,
∴△BDF≌△CEG,
∴BD=CE,
∴四边形DBCE是等对边四边形.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
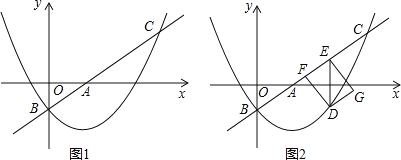
【题目】如图1,在平面直角坐标系![]() 中,直线
中,直线![]() 与x轴、y轴分别交于点A和点B(0,-1),抛物线
与x轴、y轴分别交于点A和点B(0,-1),抛物线![]() 经过点B,且与直线l的另一个交点为C(4,n).
经过点B,且与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,且点D的横坐标为t(0<t<4),DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2).若矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)M是平面内一点,将△AOB绕点M沿逆时针方向旋转90°后,得到△A'O'B',点A、O、B的对应点分别是点A'、O'、B'. 若△A'O'B'的两个顶点恰好落在抛物线上,请直接写出点A’的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形![]() 中,
中, ![]() ,垂足为
,垂足为![]() 与
与![]() 的延长线相交于
的延长线相交于![]() ,且
,且![]() ,连接
,连接![]() ;
;
(1)如图![]() ,求证:四边形
,求证:四边形![]() 是菱形;
是菱形;
(2)如图![]() ,连接
,连接![]() ,若
,若![]() ,在不添加任何辅助线的情况下,直接写出图
,在不添加任何辅助线的情况下,直接写出图![]() 中所有面积等于
中所有面积等于![]() 的面积的钝角三角形.
的面积的钝角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
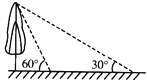
【题目】如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高_____________米(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着襄阳市近几年城市建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润![]() 与投资量
与投资量![]() 成正比例关系,如图1所示;种植花卉的利润
成正比例关系,如图1所示;种植花卉的利润![]() 与投资量
与投资量![]() 成二次函数关系,如图2所示(注:利润与投资量的单位:万元)
成二次函数关系,如图2所示(注:利润与投资量的单位:万元)
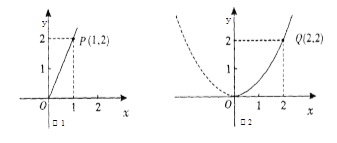
(1)分别求出利润![]() 与
与![]() 关于投资量
关于投资量![]() 的函数关系式;
的函数关系式;
(2)如果这位专业户以10万元资金投入种植花卉和树木,求他获得的最大利润是多少?
(3)在(2)的条件下,根据对市场需求的调查,这位专业户决定投入种植树木的资金不得高于投入种植花卉的资金,他至少获得多少利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证,根据图形可知他得出的这个推论指( )

A. S矩形ABMN=S矩形MNDCB. S矩形EBMF=S矩形AEFN
C. S矩形AEFN=S矩形MNDCD. S矩形EBMF=S矩形NFGD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一边是另一边的![]() 倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的 夹角叫做智慧角.
倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的 夹角叫做智慧角.
(1)在 Rt△ABC 中,∠ACB=90°,若∠A 为智慧角,则∠B 的度数为 ;
(2)如图①,在△ABC 中,∠A=45°,∠B=30°,求证:△ABC 是智慧三角形;
(3)如图②,△ABC 是智慧三角形,BC 为智慧边,∠B 为智慧角,A(3,0),点 B,C 在函数 y=![]() (x>0)的图像上,点 C 在点 B 的上方,且点 B 的纵坐标为
(x>0)的图像上,点 C 在点 B 的上方,且点 B 的纵坐标为![]() .当△ABC是直角三角形时,求 k 的值.
.当△ABC是直角三角形时,求 k 的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
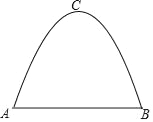
【题目】一条单车道的抛物线形隧道如图所示.隧道中公路的宽度AB=8m,隧道的最高点C到公路的距离为6m.
(1)建立适当的平面直角坐标系,求抛物线的表达式;
(2)现有一辆货车的高度是4.4m,货车的宽度是2m,为了保证安全,车顶距离隧道顶部至少0.5m,通过计算说明这辆货车能否安全通过这条隧道.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com