
【题目】若两条抛物线的顶点相同,则称它们为“友好抛物线”,抛物线C1:y1=﹣2x2+4x+2与C2:u2=﹣x2+mx+n为“友好抛物线”.
(1)求抛物线C2的解析式.
(2)点A是抛物线C2上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.
(3)设抛物线C2的顶点为C,点B的坐标为(﹣1,4),问在C2的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线C2上?若存在求出点M的坐标,不存在说明理由.

【答案】(1) u2=﹣x2+2x+3;(2) ![]() ;(3) (1,2)或(1,5).
;(3) (1,2)或(1,5).
【解析】试题分析:(1)先求得y1顶点坐标,然后依据两个抛物线的顶点坐标相同可求得m、n的值;
(2)设A(a,-a2+2a+3).则OQ=x,AQ=-a2+2a+3,然后得到OQ+AQ与a的函数关系式,最后依据配方法可求得OQ+AQ的最值;
(3)连接BC,过点B′作B′D⊥CM,垂足为D.接下来证明△BCM≌△MDB′,由全等三角形的性质得到BC=MD,CM=B′D,设点M的坐标为(1,a).则用含a的式子可表示出点B′的坐标,将点B′的坐标代入抛物线的解析式可求得a的值,从而得到点M的坐标.
试题解析:
(1)∵y1=﹣2x2+4x+2=﹣﹣2(x﹣1)2+4,
∴抛物线C1的顶点坐标为(1,4).
∵抛物线C1:与C2顶点相同,
∴![]() =1,﹣1+m+n=4.
=1,﹣1+m+n=4.
解得:m=2,n=3.
∴抛物线C2的解析式为u2=﹣x2+2x+3.
(2)如图1所示:

设点A的坐标为(a,﹣a2+2a+3).
∵AQ=﹣a2+2a+3,OQ=a,
∴AQ+OQ=﹣a2+2a+3+a=﹣a2+3a+3=﹣(a﹣![]() )2+
)2+![]() .
.
∴当a=![]() 时,AQ+OQ有最大值,最大值为
时,AQ+OQ有最大值,最大值为![]() .
.
(3)如图2所示;连接BC,过点B′作B′D⊥CM,垂足为D.

∵B(﹣1,4),C(1,4),抛物线的对称轴为x=1,
∴BC⊥CM,BC=2.
∵∠BMB′=90°,
∴∠BMC+∠B′MD=90°.
∵B′D⊥MC,
∴∠MB′D+∠B′MD=90°.
∴∠MB′D=∠BMC.
在△BCM和△MDB′中,
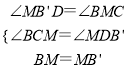 ,
,
∴△BCM≌△MDB′
∴BC=MD,CM=B′D.
设点M的坐标为(1,a).则B′D=CM=4﹣a,MD=CB=2.
∴点B′的坐标为(a﹣3,a﹣2).
∴﹣(a﹣3)2+2(a﹣3)+3=a﹣2.
整理得:a2﹣7a﹣10=0.
解得a=2,或a=5.
当a=2时,M的坐标为(1,2),
当a=5时,M的坐标为(1,5).
综上所述当点M的坐标为(1,2)或(1,5)时,B′恰好落在抛物线C2上.


科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90o,O为AB上一点,以O为圆心,OB长为半径的圆,交BC边于点D,与AC边相切于点E.
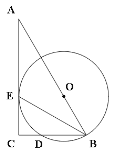
(1)求证:BE平分∠ABC;
(2)若CD︰BD=1︰2,AC=4,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)求证:BE=CF;
(2)如果AB=8,AC=6,求AE、BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“百度”搜索引擎中输入“姚明”,能搜索到与之相关的网页约27000000个,将这个数用科学记数法表示为( )
A.2.7×105
B.2.7×106
C.2.7×107
D.2.7×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数![]() 的图象为C1.二次函数
的图象为C1.二次函数![]() 的图象与C1关于y轴对称.
的图象与C1关于y轴对称.

(1)求二次函数![]() 的解析式;
的解析式;
(2)当![]() ≤0时,直接写出
≤0时,直接写出![]() 的取值范围;
的取值范围;
(3)设二次函数![]() 图象的顶点为点A,与y轴的交点为点B,一次函数
图象的顶点为点A,与y轴的交点为点B,一次函数![]() ( k,m为常数,k≠0)的图象经过A,B两点,当
( k,m为常数,k≠0)的图象经过A,B两点,当![]() 时,直接写出x的取值范围.
时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列各题:
(1)x取何值时,代数式3x+2的值不大于代数式4x+3的值?
(2)当m为何值时,关于x的方程![]() x-1=m的解不小于3?
x-1=m的解不小于3?
(3)已知不等式2(x+3)-4<0, 化简:︳4x+1︱-︱2-4x︱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明到一家文具店给全班同学购买期末考试用的2B铅笔和0.5毫米的黑色墨水签字笔. 经了解,若给全班学生每人购买1套考试用笔(1支2B铅笔和1支0.5毫米的黑色墨水签字笔为1套),只能按零售价付款,需要100元;若多购买10套考试用笔,则可以按批发价付款,同样也需要100元;小明经过计算发现按批发价购买5套考试用笔与按零售价购买4套考试用笔所付钱款数相等,小明所在班级学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com