
【题目】如图,AB为⊙O的直径,C为⊙O上一点,D、E分别是∠ACB的平分线与⊙O、AB的交点,P为AB延长线上一点,且PC=PE.试判断直线PC与⊙O的位置关系,并说明理由.
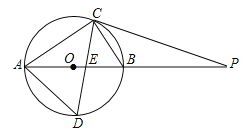
【答案】直线PC与⊙O相切.证明见解析.
【解析】试题分析:连结OC,由PC=PE得∠PCE=∠PEC,利用三角形外角性质得∠PEC=∠A+∠ACE=∠A+45°,加上∠A=90°-∠ABC,∠ABC=∠OCB,于是可得到∠PCE=90°-∠OCB+45°=90°-(∠OCE+45°)+45°,则∠OCE+∠PCE=90°,于是根据切线的判定定理可得PC为⊙O的切线
试题解析:直线PC与⊙O相切.
理由:连接OC
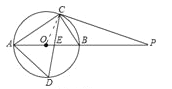
∵PC=PE
∴∠PCE=∠PEC
∴∠PCB+∠BCE=∠ACE+∠CAE
∵CD平分∠ACB
∴∠BCE=∠ACE
∴∠PCB=∠CAE
∵AB为直径
∴∠ACB=90°
∴∠CAE+∠CBA=90°
∴∠PCB+∠CBA=90°
∵OC=OB
∴∠OCB=∠CBA
∴∠PCB+∠OCB =90°,即∠OCP=90°
∴直线PC与⊙O相切.


科目:初中数学 来源: 题型:
【题目】一件商品的原价是100元,经过两次提价后的价格为121元,如果每次提价的百分率都是x,根据题意,下面列出的方程正确的是( )
A.100(1+x)=121
B.100(1﹣x)=121
C.100(1+x)2=121
D.100(1﹣x)2=121
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(﹣5,1)、(﹣1,4),结合所给的平面直角坐标系解答下列问题: 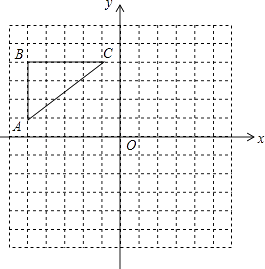
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)画出△ABC关于原点O对称的△A2B2C2;
(3)点C1的坐标是;点C2的坐标是;△ABC的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
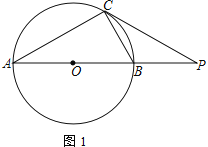
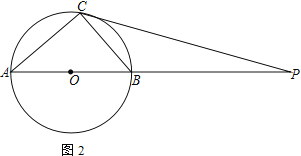
【题目】如图,⊙O为Rt△ACB的外接圆,点P是AB延长线上的一点,PC切⊙O于点C,连AC
(1)若AC=CP,求![]() 的值
的值
(2)若sin∠APC=![]() ,求tan∠ABC
,求tan∠ABC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了迎接"6.1儿童节",以调低价格的方式促销n个不同的玩具,调整后的单价y(元)与调整前的单价x(元)满足一次函数关系,如下表:
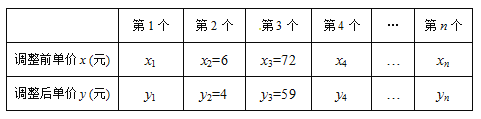
当这些玩具调整后的单价都大于2元时,解答下列问题:
(1) y与x的函数关系式为 ,x的取值范围为 ;
(2) 某个玩具调整前单价是108元,顾客购买这个玩具省了 元;
(3) 这n个玩具调整前、后的平均单价分别为![]() (元)、
(元)、![]() (元),猜想
(元),猜想![]() 与
与![]() 的关系式,并写出推导过程.
的关系式,并写出推导过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com