
 如图,四边形ABCD是正方形,点E在CB的延长线上,连结AE,将△ABE绕点A逆时针旋转90°,得到△ADF,点E落在DC上的点F处,AF的延长线交BC延长线于点G.若AB=3,AE=
如图,四边形ABCD是正方形,点E在CB的延长线上,连结AE,将△ABE绕点A逆时针旋转90°,得到△ADF,点E落在DC上的点F处,AF的延长线交BC延长线于点G.若AB=3,AE=| 13 |
| A、1.5 | B、1.6 |
| C、1.8 | D、2 |
| 13 |
| 13 |
| 13 |
| AF2-AD2 |
| CG |
| AD |
| CF |
| DF |
| CG |
| 3 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
| A、2.23×106 |
| B、2.23×108 |
| C、2.23×109 |
| D、223×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:
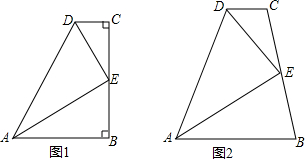 【问题情镜】
【问题情镜】查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| ||||
|
2
|
|
| 45 |
|
| 3 |
| 2 |
2
|
| 2 |
| 1 |
| 2 |
| 6 |
| 8 |
| 4 |
| 3 |
| 18 |
| 8 |
| 1 |
| 3 |
| 54 |
| 3 |
| 12 |
| 18 |
|
查看答案和解析>>
科目:初中数学 来源: 题型:

| A、被调查的学生有200人 |
| B、扇形图中公务员部分所对应的圆心角为72° |
| C、被调查的学生中喜欢其他职业的占40% |
| D、被调查的学生中喜欢教师职业的有40人 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com