
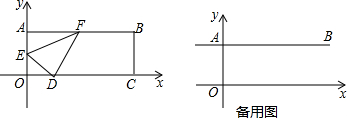
·ÖĪö £Ø1£©ČēĶ¼1£¬×÷øØÖśĻߣ¬¹¹½ØĻąĖĘČż½ĒŠĪ£¬øł¾ŻĻąĖʱČĒóDGµÄ³¤£¬ĄūÓĆ¹“¹É¶ØĄķ·Ö±šĒóDEŗĶDFµÄ³¤£¬ÓÉČż½ĒŗÆŹż¶ØŅå¼ĘĖćtan”ĻDFEµÄÖµ£»
£Ø2£©·ÖČżÖÖĒéæö£ŗ
¢Łµ±ED”ĪABŹ±£¬ČēĶ¼2£¬“ĖŹ±Ö±ĻßAB½Ų”÷DFEĖłµĆµÄČż½ĒŠĪŹĒ”÷FGH£¬
¢Śµ±DF”ĪABŹ±£¬ČēĶ¼3£¬“ĖŹ±Ö±ĻßAB½Ų”÷DFEĖłµĆµÄČż½ĒŠĪŹĒ”÷AGE£¬
¢Ūµ±EF”ĪABŹ±£¬ČēĶ¼4£¬“ĖŹ±Ö±ĻßAB½Ų”÷DFEĖłµĆµÄČż½ĒŠĪŹĒ”÷DGH£¬
“śČėĆ껿¹«Ź½Ēó³öĆ껿¼“æÉ£»
£Ø3£©·ÖĖÄÖÖĒéæö£ŗ
¢ŁČēĶ¼5£¬µ±GF=EF=$\frac{5\sqrt{13}}{3}$Ź±£¬øł¾ŻČż½ĒŗÆŹżµĆ£ŗtan”ĻG=$\frac{ED}{GD}$=$\frac{FH}{GH}$£¬Ōņ$\frac{\sqrt{13}}{3\sqrt{13}}$=$\frac{FH}{GH}$=$\frac{1}{3}$£¬ÉčFH=a£¬GH=3a£¬ŌņGF=$\sqrt{10}$a£¬Ēó³öaµÄÖµ£¬Š“³öFµÄ×ų±ź£»
¢Śµ±GF=GEŹ±£¬ČēĶ¼6£¬×÷øØÖśĻߣ¬Ö¤Ć÷”÷EFH”Õ”÷FED£¬ĒóFHŗĶOHµÄ³¤£¬Š“³öFµÄ×ų±ź£»
¢Ūµ±FG=EF=$\frac{5\sqrt{13}}{3}$Ź±£¬ČēĶ¼7£¬ĒóDGµÄ³¤£¬ĄūÓĆ¹“¹É¶ØĄķĒóEG=$\frac{\sqrt{130}}{3}$£¬ĄūÓĆĆ껿·ØĒóFHµÄ³¤£¬Š“³öFµÄ×ų±ź£»
¢Üµ±EG=EF=$\frac{5}{3}$$\sqrt{13}$Ź±£¬ČēĶ¼8£¬øł¾Żtan”ĻDFE=tan”ĻDGE=$\frac{3}{4}$=$\frac{FH}{GH}$£¬ÉčFH=3b£¬GH=4b£¬ŌņFG=5b£¬
Ēó³öbµÄÖµ£¬¼ĘĖćOHŗĶFHµÄ³¤£¬Š“³öF×ų±ź£®
½ā“š 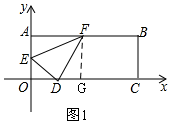 ½ā£ŗ£Ø1£©ČēĶ¼1£¬¹żF×÷FG”ĶOCÓŚG£¬ŌņFG=4£¬
½ā£ŗ£Ø1£©ČēĶ¼1£¬¹żF×÷FG”ĶOCÓŚG£¬ŌņFG=4£¬
”ßµćD£Ø3£¬0£©£¬µćE£Ø0£¬2£©£¬
”ąOE=2£¬OD=3£¬
”ßDF”ĶDE£¬
”ą”ĻEDF=90”ć£¬
”ą”ĻEDO+”ĻFDC=90”ć£¬
”ß”ĻEOD=90”ć£¬
”ą”ĻOED+”ĻEDO=90”ć£¬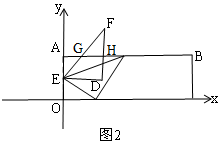
”ą”ĻOED=”ĻFDC£¬
”ß”ĻEOD=”ĻFGD=90”ć£¬
”ą”÷FDG”×”÷DEO£¬
”ą$\frac{FG}{DO}=\frac{DG}{EO}$£¬
”ą$\frac{4}{3}=\frac{DG}{2}$£¬
”ąDG=$\frac{8}{3}$£¬
Óɹ“¹É¶ØĄķµĆ£ŗDF=$\sqrt{{4}^{2}+£Ø\frac{8}{3}£©^{2}}$=$\sqrt{16+\frac{64}{9}}$=$\frac{4\sqrt{13}}{3}$£¬
ED=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$£¬
ŌŚRt”÷DEFÖŠ£¬tan”ĻDFE=$\frac{DE}{DF}$=$\frac{\sqrt{13}}{\frac{4}{3}\sqrt{13}}$=$\frac{3}{4}$£»
£Ø2£©·ÖČżÖÖĒéæö£ŗ
¢Łµ±ED”ĪABŹ±£¬ČēĶ¼2£¬“ĖŹ±Ö±ĻßAB½Ų”÷DFEĖłµĆµÄČż½ĒŠĪŹĒ”÷FGH£¬
”ßDF”ĶDE£¬
”ąAB”ĶDF£¬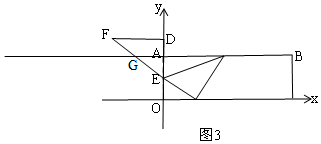
”ąDH=AE=2£¬
”ąFH=DF-DH=$\frac{4\sqrt{13}}{3}$-2£¬
ÓÉtan”ĻF=$\frac{GH}{FH}$=$\frac{3}{4}$µĆ£ŗ$\frac{GH}{\frac{4\sqrt{13}}{3}-2}$=$\frac{3}{4}$£¬
”ąGH=$\frac{2\sqrt{13}-3}{2}$£¬
”ąS=S”÷FGH=$\frac{1}{2}$GH•FH=$\frac{1}{2}$”Į$\frac{2\sqrt{13}-3}{2}$£Ø$\frac{4\sqrt{13}}{3}$-2£©=$\frac{61}{6}$-2$\sqrt{13}$£»
¢Śµ±DF”ĪABŹ±£¬ČēĶ¼3£¬“ĖŹ±Ö±ĻßAB½Ų”÷DFEĖłµĆµÄČż½ĒŠĪŹĒ”÷AGE£¬
tan”ĻAEG=$\frac{AG}{AE}=\frac{DF}{DE}$=$\frac{4}{3}$£¬
”ą$\frac{AG}{2}=\frac{4}{3}$£¬
”ąAG=$\frac{8}{3}$£¬
”ąS=S”÷AGE=$\frac{1}{2}$AG•AE=$\frac{1}{2}$”Į$\frac{8}{3}$”Į2=$\frac{8}{3}$£»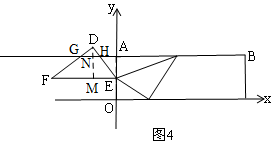
¢Ūµ±EF”ĪABŹ±£¬ČēĶ¼4£¬“ĖŹ±Ö±ĻßAB½Ų”÷DFEĖłµĆµÄČż½ĒŠĪŹĒ”÷DGH£¬
”ą”ĻF=”ĻDGH£¬
tan”ĻF=tan”ĻDGH=$\frac{DH}{DG}$=$\frac{3}{4}$£¬
ÉčDH=3x£¬DG=4x£¬ŌņGH=5x£¬
¹żD×÷DM”ĶEF£¬½»GHÓŚN£¬½»EFÓŚM£¬
”ąDN=$\frac{12}{5}$x£¬MN=AE=2£¬
ŌŚRt”÷DEFÖŠ£¬Óɹ“¹É¶ØĄķµĆ£ŗEF=$\sqrt{D{E}^{2}+D{F}^{2}}$=$\sqrt{£Ø\sqrt{13}£©^{2}+£Ø\frac{4}{3}\sqrt{13}£©^{2}}$=$\frac{5\sqrt{13}}{3}$£¬
S”÷EDF=$\frac{1}{2}$DE•DF=$\frac{1}{2}$EF•DM£¬
$\sqrt{13}$”Į$\frac{4\sqrt{13}}{3}$=$\frac{5\sqrt{13}}{3}$”ĮDM£¬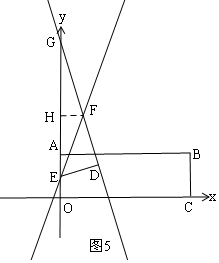
DM=$\frac{4\sqrt{13}}{5}$£¬
ÓÉDN+MN=DM£¬µĆ£ŗ$\frac{12}{5}x$+2=$\frac{4\sqrt{13}}{5}$£¬
x=$\frac{2\sqrt{13}-5}{6}$£¬
S=S”÷DGH=$\frac{1}{2}$DH”ĮDG=$\frac{1}{2}$”Į4x”Į3x=6x2=6”Į£Ø$\frac{2\sqrt{13}-5}{6}$£©2=$\frac{77}{6}$-$\frac{10\sqrt{13}}{3}$£»
£Ø3£©·ÖĖÄÖÖĒéæö£ŗ
¢ŁČēĶ¼5£¬µ±GF=EF=$\frac{5\sqrt{13}}{3}$Ź±£¬
¹żF×÷FH”ĶyÖįÓŚH£¬ŌņGH=EH£¬
Rt”÷GEDÖŠ£¬tan”ĻG=$\frac{ED}{GD}$=$\frac{FH}{GH}$£¬
”ßED=$\sqrt{3}$£¬GD=FG+DF=$\frac{5}{3}\sqrt{13}$+$\frac{4}{3}\sqrt{13}$=3$\sqrt{3}$£¬
”ą$\frac{\sqrt{13}}{3\sqrt{13}}$=$\frac{FH}{GH}$=$\frac{1}{3}$£¬
ÉčFH=a£¬GH=3a£¬ŌņGF=$\sqrt{10}$a£¬
”ą$\sqrt{10}$a=$\frac{5}{3}$$\sqrt{13}$£¬
a=$\frac{\sqrt{130}}{6}$£¬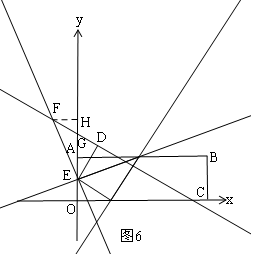
”ąFH=$\frac{\sqrt{130}}{6}$£¬
OH=OE+HE=2+3”Į$\frac{\sqrt{130}}{6}$=$\frac{\sqrt{130}}{2}$+2=$\frac{\sqrt{130}+4}{2}$£¬
”ąF£Ø$\frac{\sqrt{130}}{6}$£¬$\frac{\sqrt{130}+4}{2}$£©£»
¢Śµ±GF=GEŹ±£¬ČēĶ¼6£¬
¹żF×÷FH”ĶyÖįÓŚH£¬
”ą”ĻDFE=”ĻFEG£¬
”ß”ĻFHE=”ĻFDE=90”ć£¬EF=EF£¬
”ą”÷EFH”Õ”÷FED£¬
”ąFH=ED=$\sqrt{13}$£¬HE=DF=$\frac{4\sqrt{13}}{3}$£¬
”ąOH=EH+OE=$\frac{4\sqrt{13}}{3}$+2=$\frac{4\sqrt{13}+6}{3}$£¬
”ąF£Ø-$\sqrt{13}$£¬$\frac{4\sqrt{13}+6}{3}$£©£»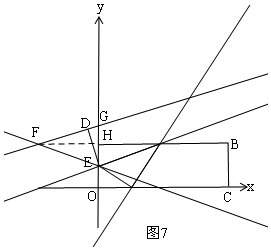
¢Ūµ±FG=EF=$\frac{5\sqrt{13}}{3}$Ź±£¬ČēĶ¼7£¬
DG=$\frac{5\sqrt{13}}{3}-\frac{4\sqrt{13}}{3}$=$\frac{\sqrt{13}}{3}$£¬
Rt”÷DEGÖŠ£¬
EG=$\sqrt{D{G}^{2}+D{E}^{2}}$=$\sqrt{£Ø\sqrt{13}£©^{2}+£Ø\frac{\sqrt{13}}{3}£©^{2}}$=$\frac{\sqrt{130}}{3}$£¬
¹żF×÷FH”ĶyÖįÓŚH£¬
”ßFG=EF£¬
”ąGH=EH=$\frac{\sqrt{130}}{6}$£¬
”ąOH=$\frac{\sqrt{130}}{6}$+2=$\frac{\sqrt{130}+12}{6}$£¬
S”÷EGF=$\frac{1}{2}$GE•FH=$\frac{1}{2}$FG•DE£¬
$\frac{\sqrt{130}}{3}$FH=$\frac{5\sqrt{13}}{3}$”Į$\sqrt{13}$£¬
$\frac{\sqrt{130}}{3}$FH=$\frac{65}{3}$£¬
FH=$\frac{\sqrt{130}}{2}$£¬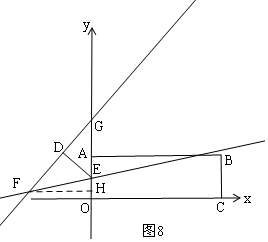
”ąF£Ø-$\frac{\sqrt{130}}{2}$£¬$\frac{\sqrt{130}+12}{6}$£©£»
¢Üµ±EG=EF=$\frac{5}{3}$$\sqrt{13}$Ź±£¬ČēĶ¼8£¬
”ą”ĻDFE=”ĻDGE£¬
”ßED”ĶGF£¬
”ąDF=DG=$\frac{4}{3}$$\sqrt{13}$£¬
”ąFG=2DF=$\frac{8}{3}\sqrt{13}$£¬
tan”ĻDFE=tan”ĻDGE=$\frac{3}{4}$=$\frac{FH}{GH}$£¬
ÉčFH=3b£¬GH=4b£¬ŌņFG=5b£¬
Ōņ5b=$\frac{8}{3}$$\sqrt{13}$£¬
b=$\frac{8}{15}$$\sqrt{13}$£¬
”ąFH=3b=3”Į$\frac{8}{15}$$\sqrt{13}$=$\frac{8}{5}\sqrt{13}$£¬GH=4b=4”Į$\frac{8}{15}\sqrt{13}$=$\frac{32}{15}\sqrt{13}$£¬
”ąOH=OE+EG-GH=OE+EF-GH=2+$\frac{5}{3}\sqrt{13}$-$\frac{32}{15}$$\sqrt{13}$=$\frac{30-7\sqrt{13}}{15}$£¬
”ąF£Ø-$\frac{8}{5}\sqrt{13}$£¬$\frac{30-7\sqrt{13}}{15}$£©£®
×ŪÉĻĖłŹö£¬µćFµÄ×ų±źĪŖ$£Ø\frac{{\sqrt{130}}}{6}£¬\frac{{\sqrt{130}+4}}{2}£©$»ņ$£Ø-\sqrt{13}£¬\frac{{4\sqrt{13}+6}}{3}£©$»ņ£Ø-$\frac{\sqrt{130}}{2}$£¬$\frac{\sqrt{130}+12}{6}$£©»ņ£Ø-$\frac{8}{5}\sqrt{13}$£¬$\frac{30-7\sqrt{13}}{15}$£©£®
µćĘĄ ±¾ĢāŹĒĖıߊĪŗĶČż½ĒŠĪµÄ×ŪŗĻĢā£¬æ¼²éĮĖČż½ĒŠĪČ«µČµÄŠŌÖŹŗĶÅŠ¶Ø”¢Čż½ĒŗÆŹż”¢¹“¹É¶ØĄķ”¢Šż×ŖµÄŠŌÖŹ”¢µČŃüČż½ĒŠĪµÄŠŌÖŹŗĶÅŠ¶ØµČÖŖŹ¶£¬±Č½Ļø“ŌÓ£¬ŌĖÓƵÄÖŖŹ¶½Ļ¶ą£¬²¢²ÉÓĆĮĖ·ÖĄąĢÖĀŪµÄĖ¼Ļė£¬ĄūÓĆŹżŠĪ½įŗĻ£¬½ā¾öĪŹĢā£¬±¾ĢāµÄ2”¢3ĪŹČŻŅ׶Ŗ½ā£¬ŅŖČĻÕęĖ¼æ¼£®


 ±øÕ½ÖŠæ¼ŗ®¼ŁĻµĮŠ“š°ø
±øÕ½ÖŠæ¼ŗ®¼ŁĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
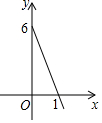 ijµĒɽ¶Ó“ó±¾ÓŖĖłŌŚµŲµÄĘųĪĀĪŖ6”ę£¬ŗ£°ĪĆæÉżøß1kmĘųĪĀĻĀ½µ6”ę£¬µĒɽ¶ÓÓÉ“ó±¾ÓŖĻņÉĻµĒøßxkmŹ±ĖūĆĒĖłŌŚĪ»ÖƵÄĘųĪĀŹĒy”ę£¬±ķŹ¾yÓėx¹ŲĻµµÄĶ¼ĻóČēĶ¼ĖłŹ¾£®
ijµĒɽ¶Ó“ó±¾ÓŖĖłŌŚµŲµÄĘųĪĀĪŖ6”ę£¬ŗ£°ĪĆæÉżøß1kmĘųĪĀĻĀ½µ6”ę£¬µĒɽ¶ÓÓÉ“ó±¾ÓŖĻņÉĻµĒøßxkmŹ±ĖūĆĒĖłŌŚĪ»ÖƵÄĘųĪĀŹĒy”ę£¬±ķŹ¾yÓėx¹ŲĻµµÄĶ¼ĻóČēĶ¼ĖłŹ¾£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
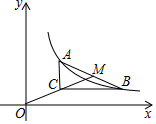 ČēĶ¼£¬ŅŃÖŖµćA£Ø2£¬n£©£¬B£Ø6£¬m£©ŹĒĖ«ĒśĻßy=$\frac{6}{x}$ÉĻµÄĮ½µć£¬·Ö±š¹żµćA£¬B ×÷x Öį£¬y ÖįµÄ“¹Ļß½»ÓŚµćC£¬OC µÄŃÓ³¤ĻßÓėAB½»ÓŚµćM£¬Ōņtan”ĻMCB=$\frac{1}{2}$£®
ČēĶ¼£¬ŅŃÖŖµćA£Ø2£¬n£©£¬B£Ø6£¬m£©ŹĒĖ«ĒśĻßy=$\frac{6}{x}$ÉĻµÄĮ½µć£¬·Ö±š¹żµćA£¬B ×÷x Öį£¬y ÖįµÄ“¹Ļß½»ÓŚµćC£¬OC µÄŃÓ³¤ĻßÓėAB½»ÓŚµćM£¬Ōņtan”ĻMCB=$\frac{1}{2}$£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
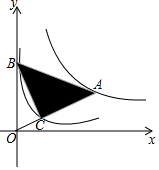 ČēĶ¼£¬µćAŹĒ·“±ČĄżŗÆŹży=$\frac{k}{x}$£Øx£¾0£©µÄĶ¼ĻóÉĻŅ»µć£¬OAÓė·“±ČĄżŗÆŹży=$\frac{1}{x}$£Øx£¾0£©µÄĶ¼Ļó½»ÓŚµćC£¬µćBŌŚyÖįµÄÕż°ėÖįÉĻ£¬ĒŅAB=OA£¬Čō”÷ABCµÄĆ껿ĪŖ6£¬ŌņkµÄÖµĪŖ9£®
ČēĶ¼£¬µćAŹĒ·“±ČĄżŗÆŹży=$\frac{k}{x}$£Øx£¾0£©µÄĶ¼ĻóÉĻŅ»µć£¬OAÓė·“±ČĄżŗÆŹży=$\frac{1}{x}$£Øx£¾0£©µÄĶ¼Ļó½»ÓŚµćC£¬µćBŌŚyÖįµÄÕż°ėÖįÉĻ£¬ĒŅAB=OA£¬Čō”÷ABCµÄĆ껿ĪŖ6£¬ŌņkµÄÖµĪŖ9£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com