练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．如图，AB，DE是⊙O的直径，点C是⊙O上的一点，且$\widehat{AD}$=$\widehat{CE}$，求证：BE=CE．

    分析 根据对顶角相等得到∠AOD=∠BOE，再根据圆心角、弧、弦的关系得$\widehat{AD}$=$\widehat{BE}$，加上$\widehat{AD}$=$\widehat{CE}$，所以$\widehat{BE}$=$\widehat{CE}$，进一步得到BE=CE．

    解答 答：BE=CE．理由如下：
    证明：∵AB、DE是⊙O的直径，
    ∴∠AOD=∠BOE，
    ∴$\widehat{AD}$=$\widehat{BE}$，
    ∵$\widehat{AD}$=$\widehat{CE}$，
    ∴$\widehat{BE}$=$\widehat{CE}$，
    ∴BE=CE．

    点评 本题考查了圆心角、弧、弦的关系：在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等．在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

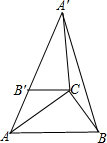    2．如图．在Rt△ABC中，∠ABC=90°，∠B=60°，BC=2，△A′B′C是由△ABC绕点C顺时针旋转得到的，其中点A′与点A是对应点，点B?与点B是对应点，已知A，B′，A′在同一条直线上．
    （1）求AA?的长；
    （2）连接A?B，求△A′BC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，已知直线l1：y=3x+1和直线l2：y=mx+n交于点P（-2，a），根据以上信息解答下列问题：
    （1）求a的值，判断直线l3：y=-$\frac{1}{2}$nx-2m是否也经过点P？请说明理由；
    （2）若l1与y轴交于点A，若l2与x轴交于点B，S△ABP=10，求直线l2的函数表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．用简便方法计算：（-8）2014×（-0.125）2015+（$\frac{1}{8}$）7×（23）6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知x+y=-3，xy=-4，代数式x+（2x-3y）+5xy-2（x-2y）+3xy的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．（1）如图，在直线l的同侧有A、B两点，在直线l上找点C、D．使AC+CB最小，DB-DA最大（保留作图痕迹）
    （2）平面直角坐标系内有两点A（-2，3），B（4，5），P是x轴上一动点，则PA+PB的最小值10，PB-PA的最大值为3$\sqrt{10}$．
    （3）根据前面两小问的处理经验，解决以下问题：
    已知a+b=5，求：
    ①代数式$\sqrt{{a}^{2}+6a+13}+\sqrt{{b}^{2}+2b+10}$的最小值；
    ②代数式$\sqrt{{b}^{2}+2b+10}-\sqrt{{a}^{2}+6a+13}$的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，在平面直角坐标系中，RT△AOB的斜边OB在x轴上，OB=$\frac{50}{3}$，点A在第一象限，∠AOB=90°且OA=10．
    （1）求A、B两点的坐标．
    （2）在平面内有一点C，使以A、B、O、C为定点的四边形为平行四边形，直接写出点C的坐标；
    （3）如图3，P、Q两点同时从A点出发，点P以每秒3个单位的速度沿着AO向O运动，点Q以每秒4个单位的速度沿着AB向B运动（P、Q同时到达终点，且运动过程中PQ始终平行x轴）．设P、Q两点运动时间为t，运动过程中，在x轴是否存在一点M，使以M、P、Q为顶点的三角形为等腰直角三角形，若存在求出t的值；若不存在说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，正方形OABC顶点AC分别在x轴y轴正半轴上A（m，0）且m是分式方程$\frac{2}{x}$=$\frac{3}{x+1}$的解，OB=$\sqrt{2}$OA．
    （1）求正方形OABC的面积；
    （2）作OD平分∠AOB交AB于D，求点D的坐标；
    （3）在（2）的条件下，过A作AE⊥OD于E，求$\frac{AE+DE}{OD}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．某地一天早晨的气温是-7℃，中午气温上升了11℃，下午又下降了9℃，晚上又下降了5℃，则晚上的温度为-10℃．

    查看答案和解析>>

    同步练习册答案