
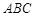 内接于圆
内接于圆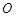 ,动点
,动点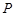 在圆上,且不与B、C重合,则
在圆上,且不与B、C重合,则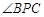 等于( )
等于( )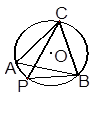
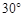 B.
B.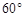 C.60°或120° D. 120°
C.60°或120° D. 120° 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
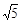 ,PB=
,PB=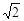 ,PC=1,求∠BPC的度数.小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图2),然后连结PP′.
,PC=1,求∠BPC的度数.小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图2),然后连结PP′.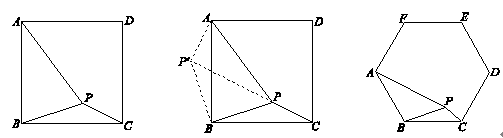
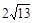 ,PB=4,PC=2,则∠BPC的度数为 ,正六边形ABCDEF的边长为 .
,PB=4,PC=2,则∠BPC的度数为 ,正六边形ABCDEF的边长为 .查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
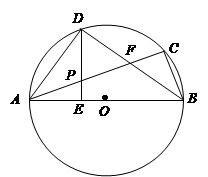
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
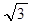 =1.732,
=1.732,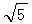 =2.236,结果精确到0.01km.)
=2.236,结果精确到0.01km.)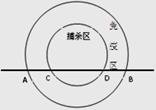
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.5,4,3 | B.10,9,8,7,6,5,4,3 |
| C.10,9,8,7,6 | D.12,11,10,9,8,7,6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com