
����Ŀ��ijУ�ڼ��С����������ļ�ֵ�ۡ��ݽ������У�������ǰ20����ѡ�ֵ��ۺϷ���m���з���ͳ�ƣ���������ʾ��
��� | ���� | Ƶ�� |
һ | 6��m��7 | 2 |
�� | 7��m��8 | 7 |
�� | 8��m��9 | a |
�� | 9��m��10 | 2 |
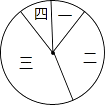
��1����a��ֵ��
��2����������ͼ���������������8��m��9������Ӧ������ͼ��Բ�ĽǴ�С��
��3�����ڵ�һ���ڵ�����ѡ�ּ�Ϊ��A1��A2 �� �ڵ������ڵ�����ѡ�ּ�Ϊ��B1��B2 �� �ӵ�һ��͵����������ѡȡ2��ѡ�ֽ��е�����̸�����һ��������1��ѡ�ֱ�ѡ�еĸ��ʣ�����״ͼ���б����г����п��ܽ������
���𰸡�
��1���⣺������ɵã�
a=20��2��7��2=9��
��a��ֵ��9
��2���⣺������ɵã�
������8��m��9������Ӧ������ͼ��Բ�Ľ�Ϊ��360��� ![]() =162��
=162��
��3���⣺������ɵã����еĿ���������ͼ��ʾ��
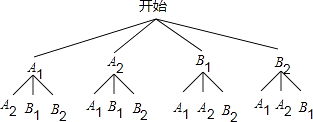
�ʵ�һ��������1��ѡ�ֱ�ѡ�еĸ����ǣ� ![]() =
= ![]() ��
��
����һ��������1��ѡ�ֱ�ѡ�еĸ����� ![]()
����������1�����ݱ���������Ϊ20�ͱ����е����ݿ������a��ֵ����2�����ݱ����е����ݿ��Եõ�������8��m��9������Ӧ������ͼ��Բ�ĽǴ�3�������������д�����еĿ����ԣ��Ӷ����Եõ���һ��������1��ѡ�ֱ�ѡ�еĸ��ʣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ�����ֻ���ѧ����ѧ�������˷��㣬ͬʱҲ������һЩ����Ӱ�죮�����������ijУ���꼶��ѧ��ȤС���ͬѧ����������������ҳ��ԡ�����ѧ�����ֻ���ѧ������Ŀ�����ͳ����������������ͼ��ͳ��ͼ�� 
��1����ε���ļҳ�������Ϊ�ˣ���ʾ������ν���ļҳ�����Ϊ�ˣ�
��2��������һ�����ܵ���ļҳ���ǡ�ó鵽������ͬ���ļҳ��ĸ�������
��3��������ͳ��ͼ�б�ʾ������ͬ�������ε�Բ�ĽǶ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У���E�ǶԽ���AC��һ�㣬��CE=CD������E��EF��AC��AD�ڵ�F������BE�� 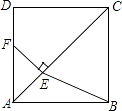
��1����֤��DF=AE��
��2����AB=2ʱ����BE2��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC �У�AB=AC=6cm����B=��C��BC=4cm���� D Ϊ AB���е㣮
��1������� P ���߶� BC ���� 1cm/s ���ٶ��ɵ� B ��� C �˶���ͬʱ���� Q ���߶� CA ���ɵ� C ��� A �˶���
������ Q ���˶��ٶ���� P ���˶��ٶ���ȣ����� 1 �����BPD ����CQP �Ƿ�ȫ�ȣ���˵�����ɣ�
������ Q ���˶��ٶ���� P ���˶��ٶȲ���ȣ����� Q ���˶��ٶ�Ϊ����ʱ���ܹ�ʹ��BPD ����CQP ȫ�ȣ�
��2������ Q �Ԣ��е��˶��ٶȴӵ� C �������� P ��ԭ�����˶��ٶȴӵ� B ͬʱ����������ʱ���ء�ABC �����˶����� �� P ��� Q ��һ���ڡ�ABC �� �������������ں�����ֱ��д���𰸣�������д������̣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC���A��B��C�䶼�ǵ��������Σ���AB=AC=5��A��B��=A��C��=3������B+��B��=90�㣬���ABC���A��B��C��������Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����MON=30�㣬��A1��A2��A3������ON�ϣ���B1��B2��B3��������OM�ϣ���A1B1A2����A2B2A3����A3B3A4����Ϊ�ȱ������Σ���OA1=1������A6B6A7�ı߳�Ϊ_____��
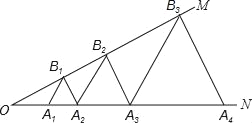
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ���꼶��ѧ��ȤС�������������AB�ĸ߶ȣ�������C�����������ﶥ�ˣ��������Ϊ48�㣬����������ķ���ǰ��6����D�����������Ϊ64�㣬������ĸ߶ȣ���������ĸ߶Ⱥ��Բ��ƣ������ȷ��0.1�ף�
���ο����ݣ�sin48��� ![]() ��tan48���
��tan48��� ![]() ��sin64���
��sin64��� ![]() ��tan64���2��
��tan64���2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx��3��a��0���Ķ���ΪE������������x�ύ��A��B���㣬��y�ύ�ڵ�C����BO=OC=3AO��ֱ��y=�� ![]() x+1��y�ύ�ڵ�D��
x+1��y�ύ�ڵ�D�� 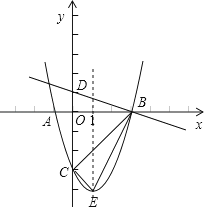
��1���������ߵĽ���ʽ��
��2��֤������DBO�ס�EBC��
��3���������ߵĶԳ������Ƿ���ڵ�P��ʹ��PBC�ǵ��������Σ������ڣ���ֱ��д������������P�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() Ϊ
Ϊ![]() �ϵ�һ����������Ҫ�������ͼ��
�ϵ�һ����������Ҫ�������ͼ��
��1����![]() ��ƽ����
��ƽ����![]() .
.
��2����![]() ��ȡһ��
��ȡһ��![]() ��ʹ��
��ʹ��![]() .
.
��3�������Խ��С�վ�����ϸ�۲�����������²������ڱ�![]() ��ȡһ��
��ȡһ��![]() ��ʹ��
��ʹ��![]() ����ʱ������
����ʱ������![]() ��
��![]() ֮�����һ����������ϵ����д��
֮�����һ����������ϵ����д��![]() ��
��![]() ��������ϵ����˵�����ɣ�
��������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com