
A.AB2=AC BC BC | B.BC2=AC AB AB | C.AC2=BC AB AB | D.AC2=2AB BC BC |
科目:初中数学 来源:不详 题型:单选题

| A.第4张 | B.第5张 | C.第6张 | D.第7张 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.DE∥BC | B.AD︰AB=DE︰BC |
| C.AD︰DB=AE︰EC | D.∠BDE+∠DBC=180° |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
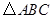 中,
中,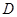 、
、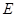 、
、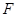 分别为三边的中点,
分别为三边的中点,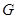 点在边
点在边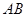 上,
上,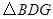 与四边形
与四边形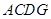 的周长相等,设
的周长相等,设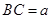 、
、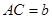 、
、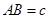 .
.
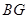 的长(用含
的长(用含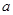 、
、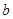 、
、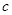 的代数式表示);
的代数式表示);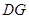 平分
平分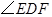 ;
;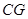 ,如本题图2,若
,如本题图2,若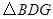 与
与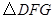 相似,求证:
相似,求证: .
.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
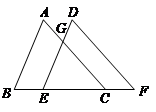
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,那么这个矩形就是一个黄金矩形。在黄金矩形ABCD的内部作一个正方形CDFE后,得到一个新的矩形ABFE,那么ABFE也是黄金矩形吗?
,那么这个矩形就是一个黄金矩形。在黄金矩形ABCD的内部作一个正方形CDFE后,得到一个新的矩形ABFE,那么ABFE也是黄金矩形吗? 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com