Question

14．定义：如果两条线段将一个三角形分成3个等腰三角形，我们把这两条线段叫做这个三角形的三分线．
（1）请你在图1中用两种不同的方法画出顶角为45°的等腰三角形的三分线，并标注每个等腰三角形顶角的度数；（若两种方法分得的三角形成3对全等三角形，则视为同一种）
（2）△ABC中，∠B=30°，AD和DE是△ABC的三分线，点D在BC边上，点E在AC边上，且AD=BD，DE=CE，设∠C=x°，试画出示意图，并直接写出x所有可能的值；
（3）如图2，△ABC中，AC=2，BC=3，∠C=2∠B，请画出△ABC的三分线，并求出三分线的长．

Answer 1

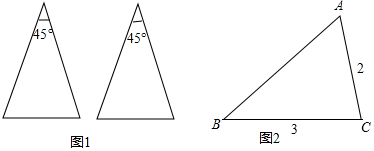
分析 （1）45°自然想到等腰直角三角形，过底角一顶点作对边的高，发现形成一个等腰直角三角形和直角三角形．直角三角形斜边的中线可形成两个等腰三角形；第二种情形以一底角作为新等腰三角形的底角，则另一底角被分为45°和22.5°，再以22.5°分别作为等腰三角形的底角或顶角，易得其中作为底角时所得的三个三角形恰都为等腰三角形；
（2）用量角器，直尺标准作30°角，而后确定一边为BA，一边为BC，根据题意可以先固定BA的长，而后可确定D点，再分别考虑AD为等腰三角形的腰或者底边，兼顾A、E、C在同一直线上，易得2种三角形ABC，根据图形易得x的值；
（3）因为∠C=2∠B，作∠C的角平分线，则可得第一个等腰三角形．而后借用圆规，以边长画弧，根据交点，寻找是否存在三分线，易得如图4图形为三分线．则可根据外角等于内角之和及腰相等等情况列出等量关系，解方程可知三分线的长．

解答 解：（1）如图所示：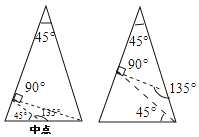


（2）如图所示：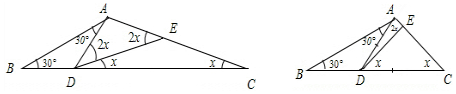

①当AD=AE时，
∵2x+x=30°+30°，
∴x=20°；
②当AD=DE时，
∵30°+30°+2x+x=180°，
∴x=40°；

（3）如图所示，CD、AE就是所求的三分线．

设∠B=α，则∠DCB=∠DCA=∠EAC=α，∠ADE=∠AED=2α，
此时△AEC∽△BDC，△ACD∽△ABC，
设AE=AD=x，BD=CD=y，
∵△AEC∽△BDC，
∴x：y=2：3，①
∵△ACD∽△ABC，
∴2：x=（x+y）：2，②
由①和②解得$\left\{\begin{array}{l}{x=\frac{2}{5}\sqrt{10}}\\{y=\frac{3}{5}\sqrt{10}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{2}{5}\sqrt{10}}\\{y=-\frac{3}{5}\sqrt{10}}\end{array}\right.$（舍去），
∴AE=$\frac{2}{5}\sqrt{10}$，CD=$\frac{3}{5}\sqrt{10}$，
即三分线的长分别为$\frac{2}{5}\sqrt{10}$和$\frac{3}{5}\sqrt{10}$．

点评 此题是相似形的综合题，主要考查了三角形内角、外角间的关系及等腰三角形知识，掌握相似三角形的判定与性质，根据成比例的线段联立方程解决问题．