
【题目】定义:有三个内角相等的四边形叫三等角四边形.
(1)三等角四边形ABCD中,∠A=∠B=∠C,求∠A的取值范围;
(2)如图,折叠平行四边形纸片DEBF,使顶点E,F分别落在边BE,BF上的点A,C处,折痕分别为DG,DH.求证:四边形ABCD是三等角四边形.
(3)三等角四边形ABCD中,∠A=∠B=∠C,若CB=CD=4,则当AD的长为何值时,AB的长最大,其最大值是多少?并求此时对角线AC的长.
【答案】
(1)
解:∵∠A=∠B=∠C,
∴3∠A+∠ADC=360°,
∴∠ADC=360°﹣3∠A.
∵0<∠ADC<180°,
∴0°<360°﹣3∠A<180°,
∴60°<∠A<120°;
(2)
证明:∵四边形DEBF为平行四边形,
∴∠E=∠F,且∠E+∠EBF=180°.
∵DE=DA,DF=DC,
∴∠E=∠DAE=∠F=∠DCF,
∵∠DAE+∠DAB=180°,∠DCF+∠DCB=180°,∠E+∠EBF=180°,
∴∠DAB=∠DCB=∠ABC,
∴四边形ABCD是三等角四边形
(3)
①当60°<∠A<90°时,如图1,
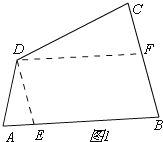
过点D作DF∥AB,DE∥BC,
∴四边形BEDF是平行四边形,∠DFC=∠B=∠DEA,
∴EB=DF,DE=FB,
∵∠A=∠B=∠C,∠DFC=∠B=∠DEA,
∴△DAE∽△DCF,AD=DE,DC=DF=4,
设AD=x,AB=y,
∴AE=y﹣4,CF=4﹣x,
∵△DAE∽△DCF,
∴ ![]() ,
,
∴ ![]() ,
,
∴y= ![]() x2+x+4=﹣
x2+x+4=﹣ ![]() (x﹣2)2+5,
(x﹣2)2+5,
∴当x=2时,y的最大值是5,
即:当AD=2时,AB的最大值为5,
②当∠A=90°时,三等角四边形是正方形,
∴AD=AB=CD=4,
③当90°<∠A<120°时,∠D为锐角,如图2,
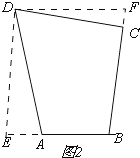
∵AE=4﹣AB>0,
∴AB<4,
综上所述,当AD=2时,AB的长最大,最大值是5;
此时,AE=1,如图3,
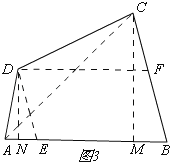
过点C作CM⊥AB于M,DN⊥AB,
∵DA=DE,DN⊥AB,
∴AN= ![]() AE=
AE= ![]() ,
,
∵∠DAN=∠CBM,∠DNA=∠CMB=90°,
∴△DAN∽△CBM,
∴ ![]() ,
,
∴BM=1,
∴AM=4,CM= ![]() =
= ![]() ,
,
∴AC= ![]() =
= ![]() =
= ![]()
【解析】(1)根据四边形的内角和是360°,确定出∠A的范围;(2)由四边形DEBF为平行四边形,得到∠E=∠F,且∠E+∠EBF=180°,再根据等角的补角相等,判断出∠DAB=∠DCB=∠ABC,即可;(3)分三种情况分别讨论计算AB的长,从而得出当AD=2时,AB最长,最后计算出对角线AC的长.此题是四边形综合题,主要考查了四边形的内角和是360°,平行四边形的性质,正方形的性质,相似三角形的性质和判定,勾股定理,解本题的关键是分类画出图形,也是解本题的难点.
【考点精析】利用勾股定理的概念和平行四边形的性质对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


科目:初中数学 来源: 题型:
【题目】阅读与计算:请阅读以下材料,并完成相应的任务.
斐波那契(约1170﹣1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果,在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的瓣数恰是斐波那契数列中的数.斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.
斐波那契数列中的第n个数可以用![]() [(
[(![]() )n﹣(
)n﹣(![]() )n]表示(其中,n≥1).这是用无理数表示有理数的一个范例.
)n]表示(其中,n≥1).这是用无理数表示有理数的一个范例.
任务:请根据以上材料,通过计算求出斐波那契数列中的第1个数和第2个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=4,M是AD的中点,点E是线段AB上一动点,连接EM并延长交线段CD的延长线于点F.
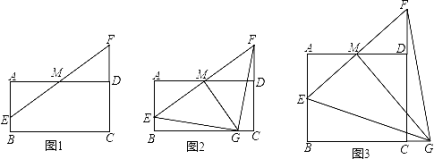
(1)如图1,求证:AE=DF;
(2)如图2,若AB=2,过点M作 MG⊥EF交线段BC于点G,求证:△GEF是等腰直角三角形
(3)如图3,若AB=![]() ,过点M作 MG⊥EF交线段BC的延长线于点G.
,过点M作 MG⊥EF交线段BC的延长线于点G.
①直接写出线段AE长度的取值范围;
②判断△GEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三组各有7名成员,测得三组成员体重数据的平均数都是58,方差分别为s甲2=36,s乙2=25.4,s丙2=16.则数据波动最小的一组是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com