
分析 (1)先化简,再合并同类项即可求解;
(2)先化简,再合并同类项即可求解.
解答 解:(1)2$\sqrt{12}$+6$\sqrt{\frac{1}{3}}$-3$\sqrt{48}$
=4$\sqrt{3}$+2$\sqrt{3}$-12$\sqrt{3}$
=-6$\sqrt{3}$;
(2)$\frac{2}{3}$$\sqrt{9x}$+6$\sqrt{\frac{x}{4}}$-2x$\sqrt{\frac{1}{x}}$
=2$\sqrt{x}$+3$\sqrt{x}$-2$\sqrt{x}$
=3$\sqrt{x}$.
点评 考查了二次根式的加减法,关键是熟练掌握二次根式的加减法法则:二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变.


科目:初中数学 来源: 题型:选择题
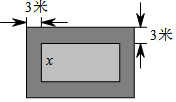 一标志性建筑的底面呈长方形,长是宽的2倍,在其四周铺上花岗岩,形成一个边宽为3米的长方形框(如图所示).已知铺这个框恰好用了504块边长为0.5米的正方向花岗岩(接缝忽略不计).若设此标志性建筑底面长方形的宽为x米,给出下列方程:
一标志性建筑的底面呈长方形,长是宽的2倍,在其四周铺上花岗岩,形成一个边宽为3米的长方形框(如图所示).已知铺这个框恰好用了504块边长为0.5米的正方向花岗岩(接缝忽略不计).若设此标志性建筑底面长方形的宽为x米,给出下列方程:| A. | ② | B. | ③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
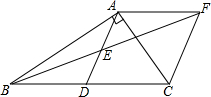 如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF,求证:四边形ADCF是菱形.
如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF,求证:四边形ADCF是菱形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
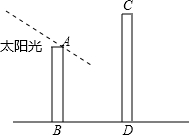 如图,AB为某一小区内的居民楼,高为18米,为缓解住房紧张的状况,现决定在这栋居民楼后面盖一栋新楼(图中CD),它的一楼是6米高的小区超市,当太阳光与水平线的夹角为30°时.
如图,AB为某一小区内的居民楼,高为18米,为缓解住房紧张的状况,现决定在这栋居民楼后面盖一栋新楼(图中CD),它的一楼是6米高的小区超市,当太阳光与水平线的夹角为30°时.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com