
 时,设以C为顶点的抛物线y=
时,设以C为顶点的抛物线y= +n与直线AB的另一交点为D(如图 2).
+n与直线AB的另一交点为D(如图 2). 
 AQC =
AQC = AOB= 90°,
AOB= 90°, ACQ=
ACQ= AOB=90°,
AOB=90°,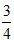 t+ 3)
t+ 3) ,
,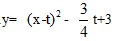 =-
=-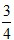 x+3,
x+3,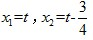 ;
; DEC=
DEC=  AOB =90°,DE// OA,
AOB =90°,DE// OA, EDC=
EDC= OAB,
OAB,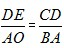 ,
,
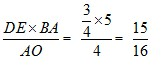
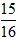 ,CD边上的高=
,CD边上的高= 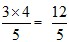 ,
,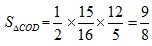 ,
,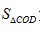 为定值;要使OC边上的高h的值最大,只要OC最短
为定值;要使OC边上的高h的值最大,只要OC最短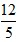 ,
, BCO=90°,
BCO=90°, AOB=90°,
AOB=90°, COP=90°-
COP=90°- BOC=
BOC= OBA,
OBA,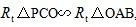
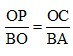 ,OP=
,OP=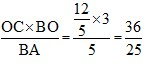 ,即t=
,即t=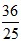 ,
,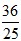 秒时,h的值最大。
秒时,h的值最大。

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
| 4 |
| 27 |
| 22 |
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com