
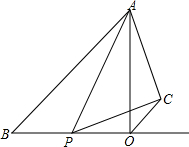
 在Rt△AOB中,∠AOB=90°,OA=OB=4厘米,点P从B出发,以1厘米/秒的速度沿射线BO运动,设点P运动时间为t(t>0)秒.△APC是以AP为斜边的等腰直角三角形,且C,O两点在直线AB的同侧,连接OC.
在Rt△AOB中,∠AOB=90°,OA=OB=4厘米,点P从B出发,以1厘米/秒的速度沿射线BO运动,设点P运动时间为t(t>0)秒.△APC是以AP为斜边的等腰直角三角形,且C,O两点在直线AB的同侧,连接OC.分析 (1)根据t=1求出BP、OP,根据勾股定理求出AP,根据余弦的定义求出AC,计算即可;
(2)根据等腰直角三角形的性质求出$\frac{AB}{AO}$=$\frac{AP}{AC}$=$\sqrt{2}$和∠BAO=∠PAC=45°,根据相似三角形的判定定理证明;
(3)分0<t<4、t=4和t>4三种情况,根据等腰直角三角形的性质和正弦的定义以及三角形的面积公式计算即可.
解答 解:(1)当t=1时,OP=3,OA=4,
在Rt△AOP中,AP=$\sqrt{O{P}^{2}+O{A}^{2}}$=5,
∵△ACP为等腰三角形,
∴AC=AP•cos45°=$\frac{5\sqrt{2}}{2}$,
∴$\frac{AC}{AO}$=$\frac{5\sqrt{2}}{8}$;
(2)证明:∵△AOB,△ACP都是等腰三角形,
∴$\frac{AB}{AO}$=$\frac{AP}{AC}$=$\sqrt{2}$,
∵∠BAO=∠PAC=45°,
∴∠BAP=∠OAC,
∴△APB∽△ACO;
(3)①当0<t<4时,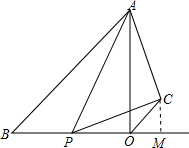
∵△APB∽△ACO,
∴$\frac{BP}{OC}$=$\frac{AB}{AO}$=$\sqrt{2}$,∠AOC=∠ABP=45°,
∴OC=$\frac{\sqrt{2}}{2}$BP=$\frac{\sqrt{2}}{2}$t,
作CM⊥BO,垂足为M,
则CM=OC•sin45°=$\frac{1}{2}$t,
∴S=$\frac{1}{2}$×OP×CM=$\frac{1}{2}$×(4-t)×$\frac{1}{2}$t=-$\frac{1}{4}$t2+t;
②当t=4时,点P与点O重合,△POC不存在;
③当t>4时,BP=t,则OP=t-4.
由①得,S=$\frac{1}{2}$×=$\frac{1}{2}$×(t-4)×$\frac{1}{2}$t=$\frac{1}{4}$t2-t;
∴S=$\left\{\begin{array}{l}{\frac{1}{4}{t}^{2}+t(0<t<4)}\\{\frac{1}{4}{t}^{2}-t(t>4)}\end{array}\right.$.
点评 本题考查的是相似三角形的判定和性质、锐角三角函数的定义以及等腰直角三角形的性质,掌握相似三角形的判定定理和性质定理、熟记锐角三角函数的定义是解题的关键.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:选择题
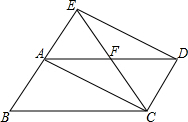 如图,将平行四边形ABCD沿对角线AC折叠,点B的对应点落在点E处,且点B、A、E在同一条直线上,CE交AD于点F,连接ED.下列结论中错误的是( )
如图,将平行四边形ABCD沿对角线AC折叠,点B的对应点落在点E处,且点B、A、E在同一条直线上,CE交AD于点F,连接ED.下列结论中错误的是( )| A. | AF=$\frac{1}{2}BC$ | B. | 四边形ACDE是矩形 | ||
| C. | 图中与△ABC全等的三角形有4个 | D. | 图中有4个等腰三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,MN是⊙O的直径,MN=2,点A在圆周上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则△PAB周长的最小值为( )
如图,MN是⊙O的直径,MN=2,点A在圆周上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则△PAB周长的最小值为( )| A. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | B. | $\frac{1}{2}$+$\sqrt{2}$ | C. | $\frac{\sqrt{3}+\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
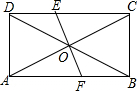 如图,在矩形ABCD中,已知AC、BD相交于O,EF⊥AC于O,且交AB于F,交CD于E,EF=AF.
如图,在矩形ABCD中,已知AC、BD相交于O,EF⊥AC于O,且交AB于F,交CD于E,EF=AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com