
分析 (1)分别利用孔明同学的测试成绩和平时成绩两项得分之和为185分,而综合评价得分为91分,分别得出等式求出答案;
(2)利用测试成绩占80%,平时成绩占20%,进而得出答案;
(3)首先假设平时成绩为满分,进而得出不等式,求出测试成绩的最小值.
解答 解:(1)设孔明同学测试成绩为x分,平时成绩为y分,依题意得:
$\left\{\begin{array}{l}x+y=185\\ 80%x+20%y=91\end{array}\right.$
解之得:$\left\{\begin{array}{l}x=90\\ y=95\end{array}\right.$
答:孔明同学测试成绩为90分,平时成绩为95分;
(2)由题意可得:80-70×80%=24,
24÷20%=120>100,故不可能.
(3)设平时成绩为满分,即100分,综合成绩为100×20%=20,
设测试成绩为a分,根据题意可得:20+80%a≥80,
解得:a≥75
答:他的测试成绩应该至少为75分.
点评 此题主要考查了一元一次不等式的应用以及二元一次方程组的应用,根据题意正确理解两种成绩所占比例是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | m$>\frac{1}{3}$ | B. | m$<\frac{1}{3}$ | C. | m$≥\frac{1}{3}$ | D. | m$≤\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
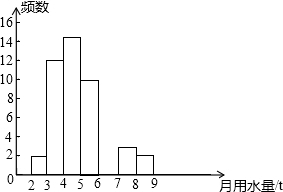 小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).| 月均用水量(单位:t) | 频数 | 百分比 |
| 2≤x<3 | 2 | 4% |
| 3≤x<4 | 12 | 24% |
| 4≤x<5 | 15 | 30% |
| 5≤x<6 | 10 | 20% |
| 6≤x<7 | 6 | 12% |
| 7≤x<8 | 3 | 6% |
| 8≤x<9 | 2 | 4% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,AD=3,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是3$\sqrt{3}$.
如图,矩形ABCD中,AD=3,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是3$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com