
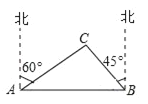
【题目】某市在新农村改造工程中需要修建一段东西方向全长1000米的道路(记作AB).已知C点周围350米范围内有一电力设施区域.在A处测得C在A的北偏东60°方向上,在B处测得C在B的北偏西45°方向上.(![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
(1)道路AB是否穿过电力设施区域?为什么?
(2)在施工250米后,为了尽量减少施工对城市交通所造成的影响,加快了施工进度,实际工作效率变成了原计划工作效率的1.5倍,结果提前5天完成了修路任务,则原计划每天修路多少米?
【答案】(1)不穿过;(2)50.
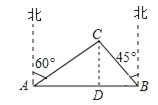
【解析】试题分析:(1)首先过点C作CD⊥AB于点D,设CD=x米,然后利用三角函数,即可表示出AD与BD的长,继而可得方程![]() x+x=1000,求得CD的长,与350米比较,即可得道路AB不穿过电力设施区域;
x+x=1000,求得CD的长,与350米比较,即可得道路AB不穿过电力设施区域;
(2)首先设原计划每天修路y米,根据题意即可得分式方程,解分式方程即可求得答案.
试题解析:解:(1)道路AB不穿过电力设施区域.
如图,过点C作CD⊥AB于点D,设CD=x米.由题意得:∠CAD=90°﹣60°=30°,∠CBD=90°﹣45°=45°.在Rt△ACD中,AD=![]() =
= ![]() (米).在Rt△BCD中,BD=CD=x(米).∵AB=1000米,∴
(米).在Rt△BCD中,BD=CD=x(米).∵AB=1000米,∴![]() x+x=1000,解得:x=500
x+x=1000,解得:x=500![]() ﹣500≈366.∵366米>350米,∴道路AB不穿过电力设施区域;
﹣500≈366.∵366米>350米,∴道路AB不穿过电力设施区域;
(2)设原计划每天修路y米,依题意得:
![]()
解得:y=50,经检验,y=50是原分式方程的解.
答:原计划每天修路50米.


科目:初中数学 来源: 题型:
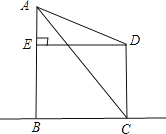
【题目】两建筑物AB和CD的水平距离为30米,如图所示,从A点测得太阳落山时,太阳光线AC照射到AB后的影子恰好在CD的墙角时的角度∠ACB=60°,又过一会儿,当AB的影子正好到达CD的楼顶D时的角度∠ADE=30°,DE⊥AB于E,则建筑物CD的高是多少米?(![]() ≈1.732,结果保留两位有效数字)
≈1.732,结果保留两位有效数字)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,回答下列问题:
数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.例如,两个有理数在数轴上对应的点之间的距离可以用这两个数的差的绝对值表示;
在数轴上,有理数3与1对应的两点之间的距离为|3-1|=2;
在数轴上,有理数5与-2对应的两点之间的距离为|5-(-2)|=7;
在数轴上,有理数-2与3对应的两点之间的距离为|-2-3|=5;
在数轴上,有理数-8与-5对应的两点之间的距离为|-8-(-5)|=3;……
如图1,在数轴上有理数a对应的点为点A,有理数b对应的点为点B,A,B两点之间的距离表示为|a-b|或|b-a|,记为|AB|=|a-b|=|b-a|.

(1)数轴上有理数-10与-5对应的两点之间的距离等于______;数轴上有理数x与-5对应的两点之间的距离用含x的式子表示为______;若数轴上有理数x与-1对应的两点A,B之间的距离|AB|=2,则x等于______;
(2)如图2,点M,N,P是数轴上的三点,点M表示的数为4,点N表示的数为-2,动点P表示的数为x.

①若点P在点M,N之间,则|x+2|+|x-4|=______;
若|x+2|+|x-4|═10,则x=______;
②根据阅读材料及上述各题的解答方法,|x+2|+|x|+|x-2|+|x-4|的最小值等于______.
查看答案和解析>>
科目:初中数学 来源: 题型:
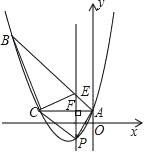
【题目】如图,已知抛物线y=![]() +bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB,AC分别交于点E,F,当四边形AECP的面积最大时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
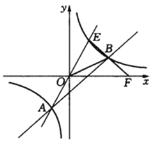
【题目】如图,直线![]() 与双曲线
与双曲线![]() 交于点A、E,AB交双曲线于另一点B(
交于点A、E,AB交双曲线于另一点B(![]() ,
,![]() ),连接EB并延长交x轴于点F.
),连接EB并延长交x轴于点F.
(1)![]() ;
;
(2)求直线AB的解析式;
(3)求△EOF的面积;
(4)若点P为坐标平面内一点,且以A,B,E,P为顶点的四边形是平行四边形,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
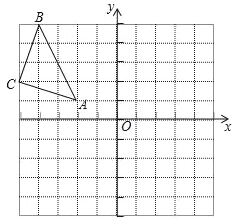
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).
(1)画出△ABC关于原点O成中心对称的△A1B1C1;
(2)写出△A1B1C1的顶点坐标;
(3)求出△A1B1C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在△ABC中,∠CAB=90°,∠CBA=50°,以AB为直径作⊙O交BC于点D,点E在边AC上,且满足ED=EA.
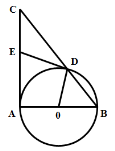
(1)求∠DOA的度数;
(2)求证:直线ED与⊙O相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有红、黄、白三种颜色的球共10个,它们除了颜色外完全相同,其中黄球个数比白球个数的3倍少2个,从袋中摸出一个球是黄球的概率为0.4.
(1)求袋中红、黄、白三种颜色的球的个数;
(2)向袋中放入若干个红球,使摸出一个球是红球的概率为0.7,求放入红球的个数;
(3)在(2)的条件下,求摸出一个球是白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)3![]() +(
+(![]() )+(
)+(![]() )+(
)+(![]() );
);
(2)25.7+(-7.3)+(-13.7)+7.3;
(3)(-2.125)+(![]() )+(
)+(![]() )+(-3.2);
)+(-3.2);
(4)(-0.8)+6.4+(-9.2)+3.6+(-1).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com