
 如图,在Rt△ABC中,∠C=90°,点D在边BC上,AD=BD=5,sin∠ADC=$\frac{4}{5}$.
如图,在Rt△ABC中,∠C=90°,点D在边BC上,AD=BD=5,sin∠ADC=$\frac{4}{5}$.分析 (1)根据正弦的概念和AD的值,求出AC和BC,得到AB的长,根据余弦概念求出答案;
(2)作MF∥AD交BC于F,根据平行线分线段成比例定理MF和DE,计算得到答案.
解答  解:(1)∵sin∠ADC=$\frac{AC}{AD}$=$\frac{4}{5}$,AD=5,
解:(1)∵sin∠ADC=$\frac{AC}{AD}$=$\frac{4}{5}$,AD=5,
∴AC=4,
由勾股定理得CD=3,
则BC=3+5=8,
由勾股定理得AB=4$\sqrt{5}$,
∴cos∠ABC=$\frac{BC}{AB}$=$\frac{2\sqrt{5}}{5}$;
(2)作MF∥AD交BC于F,
∵边AB的中点为M,
∴BF=FD=$\frac{5}{2}$,MF=$\frac{1}{2}$AD=$\frac{5}{2}$,
$\frac{DE}{MF}$=$\frac{CD}{CF}$=$\frac{6}{11}$,
∴DE=$\frac{15}{11}$,AE=5-$\frac{15}{11}$=$\frac{40}{11}$.
点评 本题考查的是解直角三角形的知识,掌握锐角三角函数的概念和平行线分线段成比例定理是解题的关键,注意辅助线的作法要准确.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:解答题
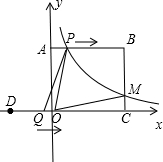 如图,平面直角坐标系(单位:cm)中,B(5,4),D(-3,0),过B作BC⊥x轴于C,BA⊥y轴于A,点P从点A出发,以每秒1cm的速度沿A→B方向向终点B运动;点Q从点D出发,以每秒2cm的速度沿D→C方向向终点C运动,已知动点P、Q同时出发,当点P,点Q有一点到达终点时,P、Q都停止运动,设运动时间为t秒.
如图,平面直角坐标系(单位:cm)中,B(5,4),D(-3,0),过B作BC⊥x轴于C,BA⊥y轴于A,点P从点A出发,以每秒1cm的速度沿A→B方向向终点B运动;点Q从点D出发,以每秒2cm的速度沿D→C方向向终点C运动,已知动点P、Q同时出发,当点P,点Q有一点到达终点时,P、Q都停止运动,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$+3$\sqrt{2}$=5$\sqrt{5}$ | B. | a8÷a2=a4 | C. | (-3a2)3=-27a6 | D. | (a2+b2)2=a4+b4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{5}$cm | B. | 4$\sqrt{5}$cm | C. | 2$\sqrt{5}$cm或4$\sqrt{5}$cm | D. | 2$\sqrt{3}$cm或4$\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在开展“国学诵读”活动中,某校为了解1300名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制如图所示的条形统计图,根据图中数据,估计该校1300名学生一周的课外阅读时间不小于7小时的人数是( )
在开展“国学诵读”活动中,某校为了解1300名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制如图所示的条形统计图,根据图中数据,估计该校1300名学生一周的课外阅读时间不小于7小时的人数是( )| A. | 600 | B. | 520 | C. | 130 | D. | 78 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m+n=6 | B. | m+n=3 | C. | m=n=3 | D. | m=2,n=4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com