
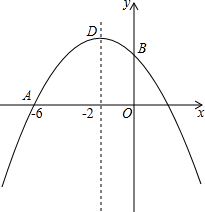
 已知抛物线y=ax2-x+c过点A(-6,0),对称轴是直线x=-2,与y轴交于点B,顶点为D.
已知抛物线y=ax2-x+c过点A(-6,0),对称轴是直线x=-2,与y轴交于点B,顶点为D.分析 (1)将对称轴是直线x=-2,以及点A(-6,0),代入解析式求出即可;
(2)过D作DH⊥x轴,利用D(-2,4),得出在Rt△DHO中tan∠AOD=2,进而得出∠AOD=∠ABO;
(3)分别根据情况1:若∠DAP=90°,情况2:若∠ADP=90°,情况3:若∠APD=90°,分析得出P点坐标即可.
解答 解:(1)∵抛物线y=ax2-x+c过点A(-6,0),对称轴为x=-2,
∴$\left\{\begin{array}{l}{36a+6+c=0}\\{-\frac{-1}{2a}=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{c=-3}\end{array}\right.$,
∴抛物线的表达式为y=-$\frac{1}{4}$x2-x+3,
顶点D坐标为(-2,4);
(2)过D作DH⊥x轴,
∵D(-2,4),
∴在Rt△DHO中tan∠AOD=2,
又∵B(0,3),A(-6,0),
∴在Rt△ABO中tan∠ABO=2,
∴∠AOD=∠ABO;
(3)∵△ADP与△AOB相似,而△AOB为直角三角形,
∴△ADP也为直角三角形,
∴情况1:若∠DAP=90°,
∵D(-2,4),A(-6,0),
∴∠DAO=45°,∴∠OAP=45°,
∴P(0,-6)
但此时AD=4$\sqrt{2}$,AP=6$\sqrt{2}$,
∴$\frac{AD}{AP}$=$\frac{2}{3}$,
又$\frac{OB}{AO}$=$\frac{1}{2}$,
∴△ADP与△AOB不相似,
∴此时点P不存在.
情况2:若∠ADP=90°,
∵D(-2,4),A(-6,0),
∴∠ADH=45°,∴∠HDP=45°,
∴P(0,2)
此时,$\frac{DP}{AD}$=$\frac{2\sqrt{2}}{4\sqrt{2}}$=$\frac{1}{2}$,$\frac{OB}{AO}$=$\frac{1}{2}$,且∠ADP=∠AOB,
∴△ADP与△AOB相似,
即当P(0,2)时,使得△ADP与△AOB相似.
情况3:若∠APD=90°,设P(0,t),
则AP2+PD2=AD2,
即36+t2+4+(t-4)2=32,得t2-4t+12=0,
∵△<0,
∴无解,
∴点P不存在.
综上所述,点P的坐标是(0,2).
点评 此题主要考查了一次函数的综合应用,涉及了待定系数法求二次函数解析式以及相似三角形的性质与判定,以及分类讨论思想的应用,根据△ADP不同角为90度分别分析求解是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
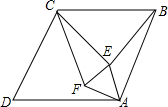 如图,在菱形ABCD中,∠D=60°,点E、F在菱形ABCD内部,△AEF为等边三角形.
如图,在菱形ABCD中,∠D=60°,点E、F在菱形ABCD内部,△AEF为等边三角形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
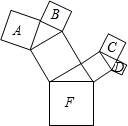 若图中正方形F以上的正方形均是以直角三角形向外作的正方形:
若图中正方形F以上的正方形均是以直角三角形向外作的正方形:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知直线l的解析式是y=$\sqrt{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2…,按此作法继续下去,则点A2014的纵坐标为($\frac{4}{3}$)2014.
如图,已知直线l的解析式是y=$\sqrt{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2…,按此作法继续下去,则点A2014的纵坐标为($\frac{4}{3}$)2014.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
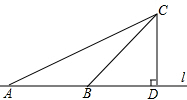 如图,某公路稽查站设立了如下测速方法:先在公路旁选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于21m,∠ACD=60°,∠BCD=30°.某辆汽车从A到B用时为2s,本路段对汽车限速为40km/h,这辆汽车是否超速?说明理由.($\sqrt{3}$≈1.732)
如图,某公路稽查站设立了如下测速方法:先在公路旁选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于21m,∠ACD=60°,∠BCD=30°.某辆汽车从A到B用时为2s,本路段对汽车限速为40km/h,这辆汽车是否超速?说明理由.($\sqrt{3}$≈1.732)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com