
分析 (1)根据四位“对称等和数”中k=4得:s≤4,t≤4,分别令s=1,2,3,4进行讨论,由$\frac{st}{2}$是整数,可得对应t的值,分别写出可能的四位数,根据能被11整除的特征:把一个数由右边向左边数,将奇位上的数字与偶位上的数字分别加起来,再求它们的差,如果这个差是11的倍数(包括0),那么,原来这个数就一定能被11整除;可知,只有2222和4400能被11整除;
(2)先根据对称等和数的定义,得2a=1+5,a=3,则A=135,设:B=$\overline{bxc}$,C=$\overline{dye}$,则b+c=2x,d+e=2y,根据已知得:$\overline{(b+d)(x+y)(c+e)}$=1665,即百位上的数字和为15或16,分情况进行讨论即可.
解答 (1)解:当s=1时,
∵$\frac{st}{2}$是整数,
∴t为偶数,
∵k=4,
∴t≤4,
∴t=2或4,
则这个四位“对称等和数”可以是:
①1223,不能被11整除,不符合条件;
②1403,不能被11整除,不符合条件;
当s=2时,
∵$\frac{st}{2}$是整数,
∴t=1,2,3,4,
则这个四位“对称等和数”可以是:
③2132,不能被11整除,不符合条件;
④2222,2222÷11=202,符合条件;
⑤2312,不能被11整除,不符合条件;
⑥2402,不能被11整除,不符合条件;
当s=3时,
∵$\frac{st}{2}$是整数,t≤4,
∴t=2或4,
则这个四位“对称等和数”可以是:
⑦3221,不能被11整除,不符合条件;
⑧3401,不能被11整除,不符合条件;
当s=4时,
同理得t=1,2,3,4,
分别为4130,4220,4310,4400,只有4400能被11整除;
综上所述,这个四位“对称等和数”有2个,分别是:2222,4400;
(2)证明:∵数A是三位“对称等和数”,且A=$\overline{1a5}$(1≤a≤9,a为整数),
∴2a=1+5,a=3,
∴A=135,
由题意设:B=$\overline{bxc}$,C=$\overline{dye}$,则b+c=2x,d+e=2y,
∵A+B+C=1800,
∴B+C=1800-135=1665,
∴$\overline{(b+d)(x+y)(c+e)}$=1665,
∴15≤b+d≤16,
①当b+d=15时,x+y=16,c+e=5,
∴b+d+c+e=15+5=20,
即2x+2y=20,
x+y=10≠16,不符合题意;
②当b+d=15时,x+y=15,c+e=15,
∴∴b+d+c+e=15+15=30,
即2x+2y=30,
x+y=15,符合题意;
∴y=-x+15,
③当b+d=16时,x+y=6,c+e=5,
∴b+d+c+e=16+5=21,
即2x+2y=21,
x+y=10.5≠6,不符合题意;
④当b+d=16时,x+y=5,c+e=15,
∴b+d+c+e=16+15=31,
即2x+2y=31,
x+y=15.5≠5,不符合题意;
综上所述,则y=-x+15.
点评 本题考查了新定义和实数的运算,比较复杂,理解对称等和数的定义是关键,注意象奇数位的对称等和数中间的数与其他数的关系:如53697是“对称等和数”,则5+7=3+9=6+6=12.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 若想检验一块儿破损的木板的两条直的边缘AB,CD是否平行,你的办法是画一条直线截线段AB与CD,测量一对同位角,如果相等,则AB∥CD,反之,则不平行.(工具不限,可结合图形进行说明,只要能说清思路即可)
若想检验一块儿破损的木板的两条直的边缘AB,CD是否平行,你的办法是画一条直线截线段AB与CD,测量一对同位角,如果相等,则AB∥CD,反之,则不平行.(工具不限,可结合图形进行说明,只要能说清思路即可)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AC⊥BD于点C,F是AB上一点,FD交AC于点E,∠B与∠D互余.
如图,AC⊥BD于点C,F是AB上一点,FD交AC于点E,∠B与∠D互余.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
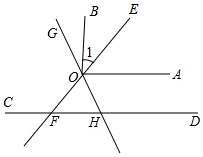 如图,OA∥CD,且分别交直线EF于O、F两点,直线GH经过O点且平分
如图,OA∥CD,且分别交直线EF于O、F两点,直线GH经过O点且平分查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com