
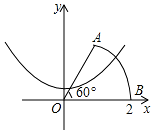
 如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴建立平面直角坐标系,点B的坐标为(2,0),扇形的圆心角是60°.若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是( )
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴建立平面直角坐标系,点B的坐标为(2,0),扇形的圆心角是60°.若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是( )| A. | -4<k<$\frac{3}{4}$ | B. | -2<k<$\frac{3}{4}$ | C. | -4<k<$\sqrt{3}$-1 | D. | -2<k<$\sqrt{3}$+1 |
分析 作AC⊥OB于C,利用正弦、余弦的概念求出点A的坐标,根据待定系数法求出直线OA的解析式,联立抛物线解析式得到抛物线与OA相切时k的值,把点B的坐标代入抛物线的解析式求出k,根据题意解答即可.
解答 解:作AC⊥OB于C,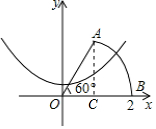
在Rt△AOC中,OC=$\frac{1}{2}$OA=1,AC=OA×sin60°=$\sqrt{3}$,
∴点A的坐标为(1,$\sqrt{3}$),
设直线OA的解析式为y=mx,则m=$\sqrt{3}$,
则直线OA的解析式为y=$\sqrt{3}$x,
联立抛物线解析式得x2+k=$\sqrt{3}$x,即x2-$\sqrt{3}$x+k=0,
△=3-4k=0,
解得k=$\frac{3}{4}$
当抛物线经过当B时,0=4+k,
解得k=-4,
∴抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是-4<k<$\frac{3}{4}$.
故选:C.
点评 本题考查的是二次函数图象与系数的关系以及软件三角函数的概念的应用,根据题意求出点A的坐标、灵活运用分情况讨论思想是解题的关键.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
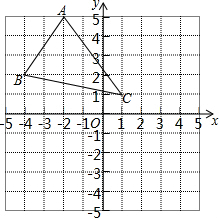 如图所示,三角形ABC的三个顶点的坐标分别是A(-2,5),B(-4,2),C(1,1),将三角形ABC向右平移3个单位长度后,再向下平移5个单位长度,可以得到三角形A′B′C′.
如图所示,三角形ABC的三个顶点的坐标分别是A(-2,5),B(-4,2),C(1,1),将三角形ABC向右平移3个单位长度后,再向下平移5个单位长度,可以得到三角形A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 请你给如图建立平面直角坐标系,使文化宫的坐标为(-3,1),超市的坐标为(2,-3).
请你给如图建立平面直角坐标系,使文化宫的坐标为(-3,1),超市的坐标为(2,-3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 分组 | 划记 | 频数 |
| 60.5~65.5 |  | 2 |
| 65.5~70.5 |  | 4 |
| 70.5~75.5 | 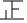 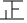 | 10 |
| 75.5~80.5 | 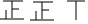 | 12 |
| 80.5~85.5 |  | 8 |
| 85.5~90.5 |  | 6 |
| 90.5~95.5 | 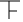 | 3 |
| 合计 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com