
分析 由函数y=kx-1与y=x2的图象交于两点(x1,y1)(x2,y2),得到x2-kx+1=0,利用根与系数的关系得出x1+x2=k,x1x2=1,代入$\frac{{y}_{2}}{{x}_{1}}$+$\frac{{y}_{1}}{{x}_{2}}$=18,得出k(k2-2)-k=18,解方程即可.
解答 解:∵函数y=kx-1与y=x2的图象交于两点(x1,y1)(x2,y2),
∴$\left\{\begin{array}{l}{y=kx-1}\\{y={x}^{2}}\end{array}\right.$,消去y得x2-kx+1=0,
∴x1+x2=k,x1x2=1,
∴$\frac{{y}_{2}}{{x}_{1}}$+$\frac{{y}_{1}}{{x}_{2}}$=$\frac{{x}_{1}{y}_{1}+{x}_{2}{y}_{2}}{{x}_{1}{x}_{2}}$=$\frac{{x}_{1}(k{x}_{1}-1)+{x}_{2}(k{x}_{2}-1)}{{x}_{1}{x}_{2}}$=$\frac{k({x}_{1}^{2}+{x}_{2}^{2})-({x}_{1}+{x}_{2})}{{x}_{1}{x}_{2}}$=18,
∴k(k2-2)-k=18,
解答k=3.
故答案为3.
点评 本题考查了二次函数与一次函数的交点问题,一元二次方程根与系数的关系,根据两个函数图象的交点坐标是相应一元二次方程的解,利用一元二次方程根与系数的关系求解是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
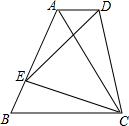 如图,四边形ABCD中,AD∥BC,AD<BC,AB=AC,点E在AB上,连接DE、DC、EC,∠DCE=∠ACB.
如图,四边形ABCD中,AD∥BC,AD<BC,AB=AC,点E在AB上,连接DE、DC、EC,∠DCE=∠ACB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>3 | B. | a<3且a≠-1 | C. | a<3 | D. | a≥3且a≠-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,Rt△ABC中,∠C=90°,AC=6,BC=8,两等圆圆A,圆B外切,那么图中两个扇形(即阴影部分)的面积之和为( )
如图所示,Rt△ABC中,∠C=90°,AC=6,BC=8,两等圆圆A,圆B外切,那么图中两个扇形(即阴影部分)的面积之和为( )| A. | $\frac{25}{4}$π | B. | $\frac{25}{8}π$ | C. | $\frac{25}{16}π$ | D. | $\frac{25}{32}π$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果一个数不是正数,那么它一定是负数 | |
| B. | 正数和负数统称有理数 | |
| C. | 分数和负数统称有理数 | |
| D. | 在有理数中,存在最小的正整数和最大的负整数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com