
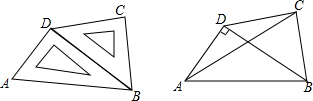
分析 (1)过点A作CD的垂线,交CD的延长线于M,作AN∥CD交BC于N,则四边形ANCM为矩形,设AM=a.由三角形ADM是等腰直角三角形,得出DM=AM=a,AD=$\sqrt{2}$a.解直角△ABD,求出AB=2AD=2a,BD=$\sqrt{3}$AD=$\sqrt{6}$a.由△CBD是等腰直角三角形,得到BC=CD=$\frac{\sqrt{2}}{2}$BD=$\sqrt{3}$a,于是AN=MC=MD+DC=($\sqrt{3}$+1)a,然后在直角△CAN中利用正切函数的定义即可求出tan∠ACB=$\frac{AN}{CN}$=$\frac{(\sqrt{3}+1)a}{a}$=$\sqrt{3}$+1;
(2)由AN=($\sqrt{3}$+1)a=6($\sqrt{3}+1$),得出a=6,于是CD=$\sqrt{3}$a=6$\sqrt{3}$.
解答 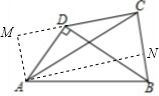 解:(1)如图,过点A作CD的垂线,交CD的延长线于M,作AN∥CD交BC于N,则四边形ANCM为矩形,设AM=a.
解:(1)如图,过点A作CD的垂线,交CD的延长线于M,作AN∥CD交BC于N,则四边形ANCM为矩形,设AM=a.
∵∠M=90°,∠ADM=180°-90°-45°=45°,
∴DM=AM=a,AD=$\sqrt{2}$a.
在△ABD中,∵∠ADB=90°,∠ABD=30°,
∴AB=2AD=2a,BD=$\sqrt{3}$AD=$\sqrt{6}$a.
在△CBD中,∵∠DCB=90°,∠CBD=45°,
∴BC=CD=$\frac{\sqrt{2}}{2}$BD=$\sqrt{3}$a,
∴AN=MC=MD+DC=a+$\sqrt{3}$a=($\sqrt{3}$+1)a.
在△CAN中,∵∠ANC=90°,CN=AM=a,AN=($\sqrt{3}$+1)a,
∴tan∠ACB=$\frac{AN}{CN}$=$\frac{(\sqrt{3}+1)a}{a}$=$\sqrt{3}$+1;
(2)∵AN=($\sqrt{3}$+1)a=6($\sqrt{3}+1$),
∴a=6,
∴CD=$\sqrt{3}$a=6$\sqrt{3}$.
点评 本题考查了解直角三角形,等腰直角三角形的判定与性质,含30°角的三边之间的关系,锐角三角函数的定义,准确作出辅助线是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
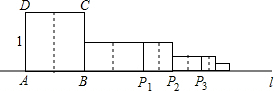 如图,正方形ABCD的边长为1,AB边与直线l重合,沿AB边的中垂线将正方形剪开,剪开后的右侧部分以B为中心,顺时针旋转90°,得到以BP1为边的新矩形,我们称之为第1次操作;沿BP1边的中垂线将矩形剪开,再将剪开后的右侧部分以点P1为中心,顺时针旋转90°,得到以P1P2为边的正方形,我们称之为第2次操作…按此规律继续操作下去,AP2016的长为AP2016=$\frac{{2}^{1010}-3}{{2}^{1008}}$.
如图,正方形ABCD的边长为1,AB边与直线l重合,沿AB边的中垂线将正方形剪开,剪开后的右侧部分以B为中心,顺时针旋转90°,得到以BP1为边的新矩形,我们称之为第1次操作;沿BP1边的中垂线将矩形剪开,再将剪开后的右侧部分以点P1为中心,顺时针旋转90°,得到以P1P2为边的正方形,我们称之为第2次操作…按此规律继续操作下去,AP2016的长为AP2016=$\frac{{2}^{1010}-3}{{2}^{1008}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
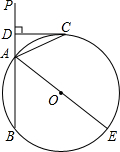 如图,AE是⊙O的直径,CD是⊙O的切线,切点为C,直线BP交⊙O于A、B两点且垂直于CD,垂足为点D,
如图,AE是⊙O的直径,CD是⊙O的切线,切点为C,直线BP交⊙O于A、B两点且垂直于CD,垂足为点D,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com