分析:选项A中,∵∠1和∠2是直线l3与l4被直线l2所截形成的内错角,由内错角相等,两直线平行,得出l3∥l4;
选项B中,∵∠3和∠4是直线l3与l4被直线l1所截形成的同位角,由同位角相等,两直线平行,得出l3∥l4;
选项D中,∵∠2和∠3是直线l1与l2被直线l4所截形成的同位角,由同位角相等,两直线平行,得出l1∥l2;
在选项C中,∠1和∠3不符合“三线八角”不能构成平行的条件,所以选项C错误.
解答:解:A、正确,∵∠1=∠2,∴l3∥l4(内错角相等,两直线平行);
B、正确,∵∠3=∠4,∴l3∥l4(同位角相等,两直线平行);
D、正确,∵∠2=∠3,∴l1∥l2(同位角相等,两直线平行).
故选C.
点评:正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.

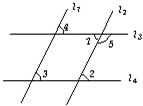 2、如图,下列说法错误的是( )
2、如图,下列说法错误的是( )

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案