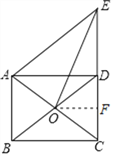
【题目】如图，矩形ABCD的对角线
相交于点O，过点A作BD的平行线交CD的延长线于点E．
求证： 
；
若
，连接OE，求
的值．
【答案】（1）证明见解析；（2）
【解析】试题分析：（1）根据矩形的对角线相等可得AC=BD，对边平行可得AB∥CD，再求出四边形ABDE是平行四边形，根据平行四边形的对边相等可得AE=BD，从而得证；
（2）如图，过点O作OF⊥CD于点F，欲求tan∠OEC的值，只需在直角△OEF中求得OF、FE的值即可．OF结合三角形中位线求得，EF结合矩形、平行四边形的性质以及勾股定理求得即可．
试题解析： 
四边形ABCD是矩形，
，
又
，
四边形ABDE是平行四边形，
，
；
如图，过点O作
于点F，
四边形ABCD是矩形，
．
，
．
同理，可得
，
．
在直角
中，由勾股定理可得： 
．
，
为
的中位线，
，
在直角
中， 
．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】在矩形ABCD中，AB=3，BC=6，P为BC边上一点，△APD为等腰三角形．
（1）小明画出了一个满足条件的△APD，其中PA=PD，如图1所示，则tan 
的值为 ；
（2）请你在图2中再画出一个满足条件的△APD（与小明的不同），并求此时tan 
的值．
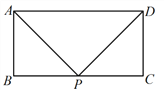
图1 图2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）先化简，再求值5x2-[2xy-3（
xy+2）+4x2]，其中x=-2，y=
（2）若（2a-1）2+|2a+b|=0，且|c-1|=2，求c（a3-b）的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
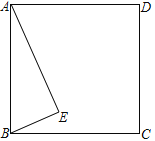
【题目】如图，正方形ABCD和直角△ABE，∠AEB＝90°，将△ABE绕点O旋转180°得到△CDF
(1) 在图中画出点O和△CDF，并简要说明作图过程
(2) 若AE＝12，AB＝13，求EF的长
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是由边长为1的小正方形组成的网格，小格的顶点叫格点，在正方形网格的三条不同的实线上各取一个格点，使其中任意两点不在同一实线上，得到格点△ABC．
（1）AC= ：△ABC是 三角形；
（2）请在下面的正方形网格中各画出一个格点直角三角形，使其中任意两点不在同一实线上，并且三个网格中的三角形互不全等．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题情境：如图1，AB∥CD， 
,
．求
度数．
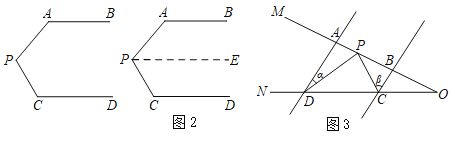
小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可得
_______．
问题迁移：如图3，AD∥BC，点P在射线OM上运动， 
， 
．
（1）当点P在A、B两点之间运动时， 
、
、
之间有何数量关系？请说明理由.
（2）如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出
、
、
之间的数量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某检修小组乘汽车沿公路检修线路，约定前进为正，后退为负．某天检修小组自A地出发到收工时所走情况如下(单位：千米)：＋10，－3，＋4，＋2，－8，＋13，－2，＋12，＋8，＋5.
(1)问：收工时距A地多远？
(2)若汽车每千米耗油0.2升，问：从A地出发到收工时汽车共耗油多少升？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知:点A是双曲线
在第一象限上的一动点，连接AO并延长交另一分支于点B，以AB为一边作等边三角形ABC，点C在第四象限，随着点A的运动，点C的位置也不断的变化，但始终在一函数图象上运动，则这个函数的解析式是( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
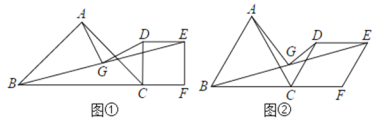
【题目】在△ABC中，AB=AC，点F是BC延长线上一点，以CF为边作菱形CDEF，使菱形CDEF与点A在BC的同侧，连接BE，点G是BE的中点，连接AG、DG．
（1）如图①，当∠BAC=∠DCF=90°时，AG与DG的位置关系为________，数量关系为________；
（2）如图②，当∠BAC=∠DCF=60°时，AG与DG的位置关系为________，数量关系为________，请证明你的结论．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com