
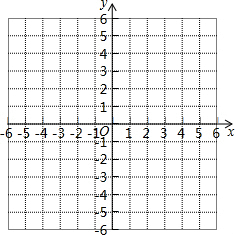
 在平面直角坐标系中,已知点A(0,-2),B(0,4).
在平面直角坐标系中,已知点A(0,-2),B(0,4).分析 (1)分别以点A、B为圆心,6为半径画弧,两弧交点即为所求,据此可得;
(2)作PD⊥AB于点D,根据等边三角形的性质及勾股定理可得PD、OD的长,即可得答案;
(3)以点P′为圆心,P′A为半径作圆,与x轴交于点C,则∠BCA=30°,再根据勾股定理求得EC的长,从而得出点C的坐标.
解答 解:(1)如图,△ABP和△ABP′即为所求作等边三角形;
(2)如图,作PD⊥AB于点D,
∵△ABP为等边三角形,AB=6,
∴PD=3$\sqrt{3}$,OD=1,
∴点P的坐标为(3$\sqrt{3}$,1),
同理可得点P′的坐标为(-3$\sqrt{3}$,1);
(3)以点P′为圆心,P′A为半径作圆,与x轴交于点C,则∠BCA=30°,
连接P′C,过点P′作P′E⊥x轴,
∵P′C=6,P′E=1,
∴EC=$\sqrt{35}$,
∴OC=$\sqrt{35}$-3$\sqrt{3}$,即点C坐标为($\sqrt{35}$-3$\sqrt{3}$,0),
同理可得点C′的坐标为($\sqrt{35}$+3$\sqrt{3}$,0).
点评 本题主要考查等边三角形判定与性质、勾股定理、圆周角定理等,熟练掌握圆周角定理确定点C的位置是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,在长14米、宽10米的矩形场地ABCD上,建有三条同样宽的小路,其中一条与AD平行,另两条与AB平行,其余的部分为草坪,已知草坪的总面积为117平方米,求小路的宽度.
如图,在长14米、宽10米的矩形场地ABCD上,建有三条同样宽的小路,其中一条与AD平行,另两条与AB平行,其余的部分为草坪,已知草坪的总面积为117平方米,求小路的宽度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | p2•2p3=2p6 | B. | (a+5)2=a2+25 | C. | $\frac{1}{a}+\frac{2}{a}=\frac{3}{a}$ | D. | $\sqrt{9}-\sqrt{4}=\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
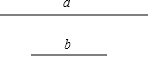 (1)用直尺和圆规作一个等腰三角形,使得底边长为线段a,底边上的高的长为线段b,要求保留作图痕迹.(不要求写出作法)
(1)用直尺和圆规作一个等腰三角形,使得底边长为线段a,底边上的高的长为线段b,要求保留作图痕迹.(不要求写出作法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,已知∠ABC=120°,AC=4
如图,在△ABC中,已知∠ABC=120°,AC=4查看答案和解析>>
科目:初中数学 来源: 题型:解答题
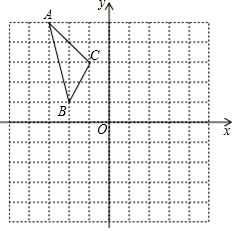 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com