
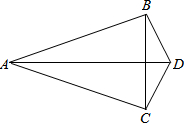
 如图,∠ABD=∠ACD=90°,∠CBD=∠BCD,则AD平分∠BAC,请说明理由.
如图,∠ABD=∠ACD=90°,∠CBD=∠BCD,则AD平分∠BAC,请说明理由.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
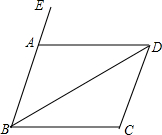 (1)如图,∠ABC与∠EAD是直线AD和直线BC被直线BE所截形成的同位角,∠ABC与∠BCD是直线AB和直线CD被直线BC所截形成的同旁内角
(1)如图,∠ABC与∠EAD是直线AD和直线BC被直线BE所截形成的同位角,∠ABC与∠BCD是直线AB和直线CD被直线BC所截形成的同旁内角查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了解某地区居民的防火意识,对该地区的初中生进行调查 | |
| B. | 为了解某商场的平均日营业额,选在周末进行调查 | |
| C. | 为了解某校1200名学生的视力情况,随机抽取该校120名学生进行调查 | |
| D. | 为了解全校学生课外小组的活动情况,对该校的男生进行调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=3,y=-6 | B. | x=-6,y=3 | C. | x=3,y=6 | D. | x=-3,y=-6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com