
【题目】如图,平行四边形![]() 中,点E是边AB的中点,延长DE交CB的延长线于点F.
中,点E是边AB的中点,延长DE交CB的延长线于点F.
(1)求证:![]() ;
;
(2)若![]() ,连接EC,则
,连接EC,则![]() 的度数是__________________
的度数是__________________

【答案】(1)见解析;(2)![]()
【解析】
(1)由平行四边形的性质得出AD∥BC,得出∠A=∠ABF,由ASA证明△ADE≌△BFE即可;
(2)由全等三角形的性质得出DE=EF,由平行四边形的性质得出AB∥DC,AB=CD,得出∠CDF=∠BEF,证出∠CDF=90°,DE=DC,由等腰直角三角形的性质得出∠DEC=∠DCE=45°,即可得出结果.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A=∠ABF,
∵点E是AB的中点,
∴AE=BE,
在△ADE和△BFE中,
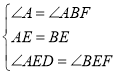 ,
,
∴△ADE≌△BFE(ASA);
(2)解:∵△ADE≌△BFE,
∴DE=EF,
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=CD,
∴∠CDF=∠BEF
∵DE⊥AB,
∴∠BEF=90°,
∴∠CDF=90°,
∵DE=AB,
∴DE=DC,
∴△DCE是等腰直角三角形,
∴∠DEC=∠DCE=45°,
∴∠FEC=135°.
故答案为:135°.


科目:初中数学 来源: 题型:
【题目】如图:等腰△ABC的底边BC长为6,面积是18,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )

A. 6 B. 8 C. 9 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的距离(即AB的长).

查看答案和解析>>
科目:初中数学 来源: 题型:
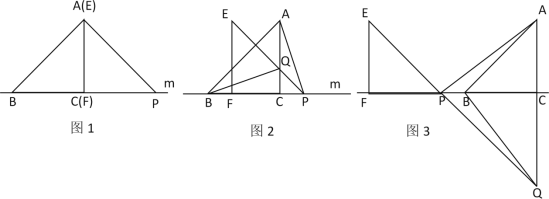
【题目】(1)问题情境,如图1,△ABC的边BC在直线m上,AC⊥BC,且AC=BC,△EFP的边FP也在直线m上,边EF与边AC重合,且EF=FP,
在图1中,AB与AP的数量关系是_______,AB与AP的位置关系是_______
(2)操作发现:将△EFP沿直线m向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ,猜想并证明BQ与AP的数量关系和位置关系
(3)猜想论证:将△EFP沿直线m向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ,(2)中的结论还成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…都是斜边在x轴上,斜边长分别为2,4,6.…的等腰直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,1),A3(0,0).则依图中所示规律,A2020的坐标为( )
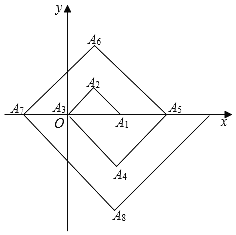
A.(2,﹣1010)B.(2,﹣1008)C.(1010,0)D.(1,1009)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荣庆公司计划从商店购买同一品牌的台灯和手电筒,已知购买一个台灯比购买一个手电筒多用20元,若用400元购买台灯和用160元购买手电筒,则购买台灯的个数是购买手电筒个数的一半.
(1)求购买该品牌一个台灯、一个手电筒各需要多少元?
(2)经商谈,商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠,如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个,且该公司购买台灯和手电筒的总费用不超过670元,那么荣庆公司最多可购买多少个该品牌台灯?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
(1)写出A、B、C的坐标.
(2)以原点O为中心,将△ABC围绕原点O逆时针旋转180°得到△A1B1C1,画出△A1B1C1.
(3)求(2)中C到C1经过的路径以及OB扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
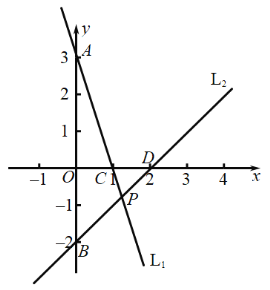
【题目】如图,L1、L2分别表示两个一次函数的图象,它们相交于点P.
(1)求出两条直线的函数关系式;
(2)点P的坐标可看作是哪个二元一次方程组的解?
(3)求出图中△APB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() 、
、![]() 两种新型节能台灯共
两种新型节能台灯共![]() 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:

(![]() )若商场预计进货款为
)若商场预计进货款为![]() 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?
(![]() )若商场规定
)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的
型台灯数量的![]() 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com