
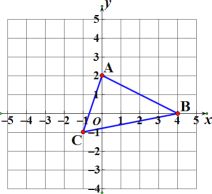
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ 1 ЕФе§ЗНаЮЭјИёжаЃЌШ§НЧаЮ ABC жаШЮвтвЛЕу P(x0ЃЌy0)ОЦНвЦКѓЖдгІЕуЮЊ P1(x0-4ЃЌy0ЃЋ3)ЃЌвбжЊ A(0ЃЌ2)ЃЌB(4ЃЌ0)ЃЌC(-1ЃЌ-1)ЃЌНЋШ§НЧаЮ ABC зїЭЌбљЕФЦНвЦЕУЕНШ§НЧаЮ A1B1C1
(1)жБНгаДГізјБъЃКA1( ЃЌ )ЃЌB1( ЃЌ )ЃЌC1( ЃЌ )ЃЛ
(2)Ш§НЧаЮ A1B1C1 ЕФУцЛ§ЮЊ ЃЛ
(3)вбжЊЕу P дк y жсЩЯЃЌЧвШ§НЧаЮ PAC ЕФУцЛ§ЕШгкШ§НЧаЮ ABC УцЛ§ЕФвЛАыЃЌЧѓ P ЕузјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉ-4ЃЌ5ЃЌ0ЃЌ3ЃЌ-5ЃЌ2ЃЛЃЈ2ЃЉ7ЃЛЃЈ3ЃЉP(0ЃЌ9)ЛђP(0ЃЌ-5)ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЕуPЕФЖдгІЕуP1зјБъжЊЃЌашНЋШ§НЧаЮЯђзѓЦНвЦ4ИіЕЅЮЛЁЂЯђЩЯЦНвЦ3ИіЕЅЮЛЃЌОнДЫПЩЕУЃЛ
ЃЈ2ЃЉжБНгРћгУИюВЙЗЈЧѓГіЁїA1B1C1ЕФУцЛ§МДПЩЃЛ
ЃЈ3ЃЉЁїPACвдPAЮЊЕзЪБЃЌИпЮЊCЕуЕНyжсЕФОрРыЃЌОнДЫПЩЕУ![]() ЃЌдйИљОнШ§НЧаЮ PAC ЕФУцЛ§ЕШгкШ§НЧаЮ ABC УцЛ§ЕФвЛАыМДПЩЧѓГіPAЕФГЄЖШЃЌгЩДЫПЩЧѓЕУPЕузјБъЃЎ
ЃЌдйИљОнШ§НЧаЮ PAC ЕФУцЛ§ЕШгкШ§НЧаЮ ABC УцЛ§ЕФвЛАыМДПЩЧѓГіPAЕФГЄЖШЃЌгЩДЫПЩЧѓЕУPЕузјБъЃЎ
НтЃКЃЈ1ЃЉ0-4=-4,2+3=5ЃЌдђA1 (-4ЃЌ5)ЃЌ
4-4=0,0+3=3ЃЌдђB1ЃЈ0ЃЌ3ЃЉЃЌ
-1-4=-5ЃЌ-1+3=2ЃЌдђC1(-5ЃЌ2ЃЉЃЛ
ЙЪД№АИЮЊЃК-4ЃЌ5ЃЌ0ЃЌ3ЃЌ-5ЃЌ2ЃЛ
ЃЈ2ЃЉШчЯТЭМЃЌ

![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК7ЃЛ
ЃЈ3ЃЉ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
гжЁпA(0ЃЌ2)ЃЌ
ЁрP(0ЃЌ9)ЛђP(0ЃЌ-5)ЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЪЧе§ЗНаЮЃЌЦфжаAЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌBЃЈ
ЃЉЃЌBЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌCЃЈ
ЃЉЃЌCЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌНЋетИіе§ЗНаЮЯђзѓЦНвЦ3ИіЕЅЮЛГЄЖШЃЌдйЯђЩЯЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЕУе§ЗНаЮ
ЃЉЃЌНЋетИіе§ЗНаЮЯђзѓЦНвЦ3ИіЕЅЮЛГЄЖШЃЌдйЯђЩЯЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЕУе§ЗНаЮ![]() ЃЎ
ЃЎ

ЃЈ1ЃЉЛГіЦНвЦКѓЕФе§ЗНаЮ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉаДГіЕуDКЭЕуDЁф ЕФзјБъЃЛ
ЃЈ3ЃЉаДГіЯпЖЮ![]() гы
гы![]() ЕФЮЛжУКЭДѓаЁЙиЯЕЃЎ
ЕФЮЛжУКЭДѓаЁЙиЯЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉЛЏМђЧѓжЕЃК![]() ЃЌЦфжаxЃНЉ
ЃЌЦфжаxЃНЉ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉаЁЭѕЙКТђСЫвЛЬзОМУЪЪгУЗПЃЌЫћзМБИНЋЕиУцЦЬЩЯЕизЉЃЌЕиУцНсЙЙШчЭМЫљЪОЃЎИљОнЭМжаЕФЪ§ОнЃЈЕЅЮЛЃКmЃЉЃЌНтД№ЯТСаЮЪЬтЃК
ЂйгУКЌxЁЂyЕФДњЪ§ЪНБэЪОГјЗПЕФУцЛ§ЪЧ_____m2ЃЛЮдЪвЕФУцЛ§ЪЧ______m2
ЂкаДГігУКЌxЁЂyЕФДњЪ§ЪНБэЪОетЬзЗПЕФзмУцЛ§ЪЧЖрЩйЦНЗНУзЃП
ЂлЕБx=3ЃЌy=2ЪБЃЌЧѓетЬзЗПЕФзмУцЛ§ЪЧЖрЩйЦНЗНУзЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЗЩЛњзХТНКѓЛЌааЕФОрРыSЃЈЕЅЮЛЃКmЃЉгыЛЌааЕФЪБМфtЃЈЕЅЮЛЃКsЃЉЕФКЏЪ§ЙиЯЕЪНЪЧS=80tЉ2t2 ЃЌ ЗЩЛњзХТНКѓЛЌааЕФзюдЖОрРыЪЧmЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцзХЁАЕЭЬМЩњЛюЁЂТЬЩЋГіааЁБРэФюЕФЦеМАЃЌаТФмдДЦћГЕдкж№НЅГЩЮЊШЫУЧЯВАЎЕФНЛЭЈЙЄОпЃЌФГЦћГЕЯњЪлЙЋЫОМЦЛЎЙКНјвЛХњаТФмдДЦћГЕГЂЪдНјааЯњЪлЃЌОнСЫНтЃЌ2СОAаЭЦћГЕЃЌ3СОBаЭЦћГЕЕФНјМлЙВМЦ80ЭђдЊЃЛ3СНAаЭЦћГЕЃЌ2СНBаЭЦћГЕЕФНјМлЙВМЦ95ЭђдЊЃЎ
ЃЈ1ЃЉЮЪAЁЂBСНжжаЭКХЕФЦћГЕУПСОНјМлЗжБ№ЮЊЖрЩйЭђдЊЃП
ЃЈ2ЃЉШєИУЙЋЫОМЦЛЎгУ200ЭђдЊЙКНјвдЩЯСНжжаЭКХЕФаТФмдДЦћГЕЃЈСНжжаЭКХЕФЦћГЕОљЙКТђЃЉЧыФуАяжњИУЙЋЫОЩшМЦЙКТђЗНАИЃЛ
ЃЈ3ЃЉШєИУЦћГЕЯњЪлЙЋЫОЯњЪл1СОAаЭЦћГЕПЩЛёРћ800дЊЃЌЯњЪл1СОBаЭЦћГЕПЩЛёРћ500дЊЃЛдкЂкЕФЙКТђЗНАИжаЃЌМйШчетаЉаТФмдДЦћГЕШЋВПЪлГіЃЌФФжжЗНАИЛёРћзюДѓЃПзюДѓРћШѓЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯABC=90ЁуЃЌBC=6ЃЌDЮЊACбгГЄЯпЩЯвЛЕуЃЌAC=3CDЃЌЙ§ЕуDзїDHЁЮABЃЌНЛBCЕФбгГЄЯпгкЕуHЃЎ
ЃЈ1ЃЉЧѓBHЕФГЄЃЛ
ЃЈ2ЃЉШєAB=12ЃЌЪдХаЖЯЁЯCBDгыЁЯAЕФЪ§СПЙиЯЕЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌABCDЕФЖЅЕуЕФзјБъЗжБ№ЮЊAЃЈЉ6ЃЌ9ЃЉЃЌBЃЈ0ЃЌ9ЃЉЃЌCЃЈ3ЃЌ0ЃЉЃЌDЃЈЉ3ЃЌ0ЃЉЃЌХзЮяЯпy=ax2+bx+cЃЈaЃЌbЃЌcЮЊГЃЪ§ЃЌЧвaЁй0ЃЉЙ§AЁЂBСНЕуЃЌЖЅЕуЮЊMЃЎ
ЃЈ1ЃЉШєХзЮяЯпЙ§ЕуCЃЌЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєХзЮяЯпЕФЖЅЕуMТфдкЁїACDЕФФкВПЃЈАќРЈБпНчЃЉЃЌЧѓaЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉШєaЃМ0ЃЌСЌНсCMНЛЯпЖЮABгкЕуQЃЈQВЛгыЕуBжиКЯЃЉЃЌСЌНгDMНЛЯпЖЮABгкЕуPЃЌЩшS1=SЁїADP+SЁїCBQ ЃЌ S2=SЁїMPQ ЃЌ ЪдХаЖЯS1гыS2ЕФДѓаЁЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк8ЁС8ЕФЭјИёжаЕФУПИіаЁе§ЗНаЮБпГЄЖМЪЧ1ЃЌЯпЖЮНЛЕуГЦзїИёЕуЃЎШЮвтСЌНгетаЉИёЕуЃЌПЩЕУЕНвЛаЉЯпЖЮЃЎАДвЊЧѓзїЭМЃК
(1)ЧыЛГіЁїABCЕФИпADЃЛ
(2)ЧыСЌНгИёЕуЃЌгУвЛЬѕЯпЖЮНЋЭМжаЁїABCЗжГЩУцЛ§ЯрЕШЕФСНВПЗжЃЛ
(3)жБНгаДГіЁїABCЕФУцЛ§ЪЧ_____________.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌCA=12 ![]() cmЃЌBC=12cmЃЛЖЏЕуPДгЕуCПЊЪМбиCAвд2
cmЃЌBC=12cmЃЛЖЏЕуPДгЕуCПЊЪМбиCAвд2 ![]() cm/sЕФЫйЖШЯђЕуAвЦЖЏЃЌЖЏЕуQДгЕуAПЊЪМбиABвд4cm/sЕФЫйЖШЯђЕуBвЦЖЏЃЌЖЏЕуRДгЕуBПЊЪМбиBCвд 2cm/sЕФЫйЖШЯђЕуCвЦЖЏЃЎШчЙћPЁЂQЁЂRЗжБ№ДгCЁЂAЁЂBЭЌЪБвЦЖЏЃЌвЦЖЏЪБМфЮЊtЃЈ0ЃМtЃМ6ЃЉsЃЎ
cm/sЕФЫйЖШЯђЕуAвЦЖЏЃЌЖЏЕуQДгЕуAПЊЪМбиABвд4cm/sЕФЫйЖШЯђЕуBвЦЖЏЃЌЖЏЕуRДгЕуBПЊЪМбиBCвд 2cm/sЕФЫйЖШЯђЕуCвЦЖЏЃЎШчЙћPЁЂQЁЂRЗжБ№ДгCЁЂAЁЂBЭЌЪБвЦЖЏЃЌвЦЖЏЪБМфЮЊtЃЈ0ЃМtЃМ6ЃЉsЃЎ
ЃЈ1ЃЉЁЯCABЕФЖШЪ§ЪЧЃЛ
ЃЈ2ЃЉвдCBЮЊжБОЖЕФЁбOгыABНЛгкЕуMЃЌЕБtЮЊКЮжЕЪБЃЌPMгыЁбOЯрЧаЃП
ЃЈ3ЃЉаДГіЁїPQRЕФУцЛ§SЫцЖЏЕувЦЖЏЪБМфtЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓSЕФзюаЁжЕМАЯргІЕФtжЕЃЛ
ЃЈ4ЃЉЪЧЗёДцдкЁїAPQЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧѓГіЯргІЕФtжЕЃЛШєВЛДцдкЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com