
 已知:抛物线y=x2+2(k+1)x+k2+2k.
已知:抛物线y=x2+2(k+1)x+k2+2k.分析 (1)根据原式等于0,利用根的判别式△>0即可得出答案;
(2)根据抛物线解析式求得电费A、B、C的坐标,利用三角形的面积公式可以求得△ABC的面积.
解答 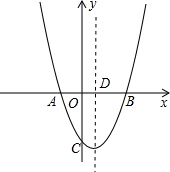 (1)解:令y=0,则x2+2(k+1)x+k2+2k=0,
(1)解:令y=0,则x2+2(k+1)x+k2+2k=0,
∴△=4(k+1)2-4(k2+2k)=4>0,
∴无论k取任何实数,抛物线与x轴总有两个交点.
(2)证明:解方程 x2+2(k+1)x+k2+2k=0,
得 x=-k,或x=-k-2.
∴A(-k-2,0),B(-k,0).
∴AB=2.
∴AB的中点D(-k-1,0).
当x=-k-1时,y=-1.
∴点C的纵坐标yc=-1.
∴S△ABC=$\frac{1}{2}$AB×|yc|=1.
∴无论k取任何实数,△ABC的面积总为确定的值.
点评 本题考查了二次函数y=ax2+bx+c的交点与一元二次方程ax2+bx+c=0根之间的关系,抛物线与坐标轴交点坐标的求法,三角形的面积,难度适中.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲队 | B. | 两队一样整齐 | C. | 乙队 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “奔跑吧,兄弟”节目的收视率 | B. | “神州十一号”飞船的零件合格率 | ||
| C. | 某种品牌节能灯的使用寿命 | D. | 全国植树节中栽植树苗的成活率 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线l1:y=-2x与直线l2:y=kx+b在同一平面直角坐标系内交于点P.
如图,直线l1:y=-2x与直线l2:y=kx+b在同一平面直角坐标系内交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,过点A(2,0)的直线l与y轴交于点B,tan∠OAB=$\frac{1}{2}$,直线l上的点P位于y轴左侧,且到y轴的距离为1.
如图,在平面直角坐标系中,过点A(2,0)的直线l与y轴交于点B,tan∠OAB=$\frac{1}{2}$,直线l上的点P位于y轴左侧,且到y轴的距离为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com