

 ,AB=4。∴点B的坐标为(4
,AB=4。∴点B的坐标为(4 ,4)。………2分
,4)。………2分 轴,∴AB∥EC。 又∵△OBC是等边三角形,∴OC=OB=8。
轴,∴AB∥EC。 又∵△OBC是等边三角形,∴OC=OB=8。 ,则由折叠对称的性质,得GA=GC=8-
,则由折叠对称的性质,得GA=GC=8- 。
。  ,即
,即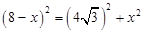 ,
, 。∴OG的长为1。………………………………………………………………10分
。∴OG的长为1。………………………………………………………………10分 )2,解此方程即可求得OG的长.
)2,解此方程即可求得OG的长.

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.两条对角线相等的四边形是矩形 |
| B.两条对角线互相垂直的四边形是菱形 |
| C.两条对角线互相垂直且相等的四边形是正方形 |
| D.两条对角线互相平分的四边形是平行四边形 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 轴于点F(如图).设动点P、Q运动时间为t(单位:秒),则:
轴于点F(如图).设动点P、Q运动时间为t(单位:秒),则:
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹);
的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹); 的位置关系,并说明理由;
的位置关系,并说明理由; 与AC边的另一个交点为F,
与AC边的另一个交点为F,
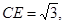 求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)
求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com